 por gjmiquel » Ter Nov 29, 2011 13:12
por gjmiquel » Ter Nov 29, 2011 13:12
Seja

uma função duas vezes diferenciável, tal que
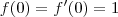
e
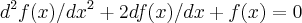
. Se
![A=ln[f(4)/9] A=ln[f(4)/9]](/latexrender/pictures/591655eaf7758ec794b500e2057c19bc.png)
, calcule o valor de
![\alpha=\left[{A\int_{0}^1e^{t}f(t)dt}\right]^2 \alpha=\left[{A\int_{0}^1e^{t}f(t)dt}\right]^2](/latexrender/pictures/c756e4129eebeb559242771efc73dd1b.png)
.
Eu tentei diversas abordagens. A mais lógica e direta foi trabalhar através da expansão de Taylor, e dessa forma obter uma expressão para a função f(x). Outra abordágem foi trabalhar inicialmente através da integral definida. No entanto, em ambas as abordagens, o que causa um pouco de desconforto (hehehe) é que a expressão obtida para f(x) garante que f(4) seja um número negativo.
Alguma ajuda?
-
gjmiquel
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 29, 2011 12:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: formado
 por LuizAquino » Ter Nov 29, 2011 14:43
por LuizAquino » Ter Nov 29, 2011 14:43
gjmiquel escreveu:Seja
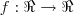
uma função duas vezes diferenciável, tal que
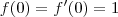
e
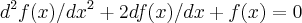
. Se
![A=ln[f(4)/9] A=ln[f(4)/9]](/latexrender/pictures/591655eaf7758ec794b500e2057c19bc.png)
, calcule o valor de
![\alpha=\left[{A\int_{0}^1e^{t}f(t)dt}\right]^2 \alpha=\left[{A\int_{0}^1e^{t}f(t)dt}\right]^2](/latexrender/pictures/c756e4129eebeb559242771efc73dd1b.png)
.
gjmiquel escreveu:Eu tentei diversas abordagens. A mais lógica e direta foi trabalhar através da expansão de Taylor, e dessa forma obter uma expressão para a função f(x). Outra abordágem foi trabalhar inicialmente através da integral definida. No entanto, em ambas as abordagens, o que causa um pouco de desconforto (hehehe) é que a expressão obtida para f(x) garante que f(4) seja um número negativo.
Alguma ajuda?
Primeiro resolva a
EDO linear de 2ª ordem:
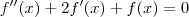
, sendo que
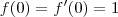
.
Após resolver a EDO você vai encontrar que
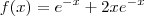
.
A partir daí fica fácil concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por gjmiquel » Qua Nov 30, 2011 09:14
por gjmiquel » Qua Nov 30, 2011 09:14
Muito obrigado. Minha cabeça parece não ter funcionado direito.....hehehehhe
Muito obrigado mesmo...
-
gjmiquel
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 29, 2011 12:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2593 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- Questão de concurso pmpe 2009 38
por Raphael Feitas10 » Qua Nov 09, 2011 01:24
- 5 Respostas
- 4097 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 14, 2012 21:43
Sistemas de Equações
-
- UFF 2009
por Bernar » Qui Nov 26, 2009 23:19
- 1 Respostas
- 2854 Exibições
- Última mensagem por Molina

Sex Nov 27, 2009 13:05
Progressões
-
- Exercício UFG 2009-1
 por wdcardoso » Sex Abr 13, 2012 22:46
por wdcardoso » Sex Abr 13, 2012 22:46
- 5 Respostas
- 3276 Exibições
- Última mensagem por wdcardoso

Sáb Abr 14, 2012 21:12
Geometria Plana
-
- Problema (UNISC 2009)
por Karina » Qui Mar 25, 2010 20:35
- 2 Respostas
- 2574 Exibições
- Última mensagem por Karina

Sáb Mar 27, 2010 13:50
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 uma função duas vezes diferenciável, tal que
uma função duas vezes diferenciável, tal que 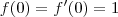 e
e 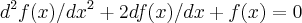 . Se
. Se ![A=ln[f(4)/9] A=ln[f(4)/9]](/latexrender/pictures/591655eaf7758ec794b500e2057c19bc.png) , calcule o valor de
, calcule o valor de ![\alpha=\left[{A\int_{0}^1e^{t}f(t)dt}\right]^2 \alpha=\left[{A\int_{0}^1e^{t}f(t)dt}\right]^2](/latexrender/pictures/c756e4129eebeb559242771efc73dd1b.png) .
.

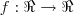 uma função duas vezes diferenciável, tal que
uma função duas vezes diferenciável, tal que 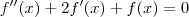 , sendo que
, sendo que 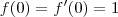 .
.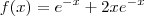 .
.