 por beel » Dom Nov 20, 2011 22:08
por beel » Dom Nov 20, 2011 22:08
pra resolver essa integral por substituiçao
![\int_{1}^{2}x^3\sqrt[]{x^2 + 1}dx \int_{1}^{2}x^3\sqrt[]{x^2 + 1}dx](/latexrender/pictures/fef2e834b0bec0c6cf1b61e2fed977e0.png)
tomei o "u" como x³, mas meu resultado deu muito errado... o u é esse mesmo?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Ter Nov 22, 2011 13:29
por beel » Ter Nov 22, 2011 13:29
Nessa ultima parte, nao teria que multiplicar (u-1) por x? ja que é x³ ( e x²= u -1 )
minha resposta ta o seguinte por enquanto:
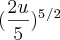
-
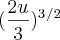
...ai apliquei isso em 5 e depois em 2,
mas minha resposta deu um numero gigante com raiz inexata
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Ter Nov 22, 2011 19:14
por MarceloFantini » Ter Nov 22, 2011 19:14
Não, não tem pois eu já usei o x "extra" na mudança de variável, então não está faltando nada. E sim, a resposta é grande com números irracionais. Faltou um 2 dividindo tudo na minha resolução, conserte quando for resolver.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por beel » Dom Nov 27, 2011 15:50
por beel » Dom Nov 27, 2011 15:50
minha resposta deu isso...
![\frac{1}{2}((\frac{2}{5}(\sqrt[]{3125}- \sqrt[]{32}) - \frac{2}{3}(\sqrt[]{125} - \sqrt[]{8})) \frac{1}{2}((\frac{2}{5}(\sqrt[]{3125}- \sqrt[]{32}) - \frac{2}{3}(\sqrt[]{125} - \sqrt[]{8}))](/latexrender/pictures/d39d90eacba9df4e0aa38cfaf066b01f.png)
verifiquei naquele site que voce ja sugeriu, mas lá o resultado é uma aproximação com numeros decimais e precisava da resposta em fração...na verdade nas alternativas das respostas,todas possuem tem raiz cubica e denominador 8, tentei chegar em alguma resposta assim mas nao consegui
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4531 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3684 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Cálculo de integral
por LAZAROTTI » Dom Set 30, 2012 19:52
- 0 Respostas
- 1195 Exibições
- Última mensagem por LAZAROTTI

Dom Set 30, 2012 19:52
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de integral
por jmario » Ter Mai 18, 2010 12:25
- 1 Respostas
- 3274 Exibições
- Última mensagem por MarcosFreitas

Qua Jun 02, 2010 13:04
Cálculo: Limites, Derivadas e Integrais
-
- CALCULO DE INTEGRAL
por Jaison Werner » Sex Jan 07, 2011 18:58
- 4 Respostas
- 3168 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 08, 2011 12:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{2}x^3\sqrt[]{x^2 + 1}dx \int_{1}^{2}x^3\sqrt[]{x^2 + 1}dx](/latexrender/pictures/fef2e834b0bec0c6cf1b61e2fed977e0.png)

![\int_{1}^{2}x^3\sqrt[]{x^2 + 1}dx \int_{1}^{2}x^3\sqrt[]{x^2 + 1}dx](/latexrender/pictures/fef2e834b0bec0c6cf1b61e2fed977e0.png)


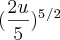 -
- 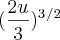 ...ai apliquei isso em 5 e depois em 2,
...ai apliquei isso em 5 e depois em 2,


![\frac{1}{2}((\frac{2}{5}(\sqrt[]{3125}- \sqrt[]{32}) - \frac{2}{3}(\sqrt[]{125} - \sqrt[]{8})) \frac{1}{2}((\frac{2}{5}(\sqrt[]{3125}- \sqrt[]{32}) - \frac{2}{3}(\sqrt[]{125} - \sqrt[]{8}))](/latexrender/pictures/d39d90eacba9df4e0aa38cfaf066b01f.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.