 por plugpc » Qua Mai 20, 2009 19:31
por plugpc » Qua Mai 20, 2009 19:31
1.Se a e b são números positivos tais que

e

o valor de a:
a) 9
b)

c)
![\sqrt[9]{9} \sqrt[9]{9}](/latexrender/pictures/437abc99dfab74ed59bfaed7b8a07785.png)
d)
![\sqrt[3]{9} \sqrt[3]{9}](/latexrender/pictures/32fa931f3d4f8b1110acfdbbe9d2b6d2.png)
e)
![\sqrt[4]{9} \sqrt[4]{9}](/latexrender/pictures/d15056f249065b7a7cfca03c9e5e5cb3.png)
2. Se os números x=
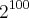
, y=375 e z=
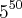
são orde-nados em ordem crescente, a sequencia correta é
a) x, y, z
b) x,z,y
c) y,x,z
d) y,z, x
e) z, y, x
Gostaria mais uma vez da sua ajuda com esses problemas pois não sei ainda como resolvê-los.
Obrigado por todos os outros que você já me ajudou...
-
plugpc
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 07, 2008 22:00
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matemática
- Andamento: cursando
 por Marcampucio » Qua Mai 20, 2009 20:30
por Marcampucio » Qua Mai 20, 2009 20:30
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Marcampucio » Qua Mai 20, 2009 20:40
por Marcampucio » Qua Mai 20, 2009 20:40
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Molina » Qua Mai 20, 2009 22:39
por Molina » Qua Mai 20, 2009 22:39
Marcampucio escreveu:1)

sendo

![\\log(a^b)=log(b^a)\\blog(a)=alog(b)\\\frac{b}{a}=\frac{log(b)}{log(a)}\\\frac{b}{a}=log_a(b)\\9=log_a(9a)\\a^9=9a\\a^8=9\\a=\sqrt[8]{9} \\log(a^b)=log(b^a)\\blog(a)=alog(b)\\\frac{b}{a}=\frac{log(b)}{log(a)}\\\frac{b}{a}=log_a(b)\\9=log_a(9a)\\a^9=9a\\a^8=9\\a=\sqrt[8]{9}](/latexrender/pictures/3948cfc71c8bd408dcf30bb2ada655d7.png)
Boa noite.
Refiz a conta bateu no mesmo resultado.
Estranho não ter essa resposta nas alternativas que ela passou..
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Se os números reais positivos x e y forem tais que:
 por andersontricordiano » Seg Abr 11, 2011 15:25
por andersontricordiano » Seg Abr 11, 2011 15:25
- 7 Respostas
- 5709 Exibições
- Última mensagem por FilipeCaceres

Ter Abr 12, 2011 12:31
Logaritmos
-
- Divisão de inteiros positivos
por DanielFerreira » Dom Set 16, 2012 20:59
- 2 Respostas
- 5995 Exibições
- Última mensagem por DanielFerreira

Dom Set 16, 2012 21:12
Desafios Médios
-
- [Quantidade de divisores positivos]
por Gustavo Gomes » Seg Dez 17, 2012 22:44
- 2 Respostas
- 1941 Exibições
- Última mensagem por Gustavo Gomes

Ter Dez 18, 2012 21:32
Teoria dos Números
-
- Teorema inteiros positivos
por Jovani Souza » Sex Jun 07, 2013 18:05
- 0 Respostas
- 1229 Exibições
- Última mensagem por Jovani Souza

Sex Jun 07, 2013 18:05
Sequências
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17201 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e 

![\sqrt[9]{9} \sqrt[9]{9}](/latexrender/pictures/437abc99dfab74ed59bfaed7b8a07785.png)
![\sqrt[3]{9} \sqrt[3]{9}](/latexrender/pictures/32fa931f3d4f8b1110acfdbbe9d2b6d2.png)
![\sqrt[4]{9} \sqrt[4]{9}](/latexrender/pictures/d15056f249065b7a7cfca03c9e5e5cb3.png)
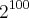 , y=375 e z=
, y=375 e z=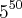 são orde-nados em ordem crescente, a sequencia correta é
são orde-nados em ordem crescente, a sequencia correta é 

 sendo
sendo ![\\log(a^b)=log(b^a)\\blog(a)=alog(b)\\\frac{b}{a}=\frac{log(b)}{log(a)}\\\frac{b}{a}=log_a(b)\\9=log_a(9a)\\a^9=9a\\a^8=9\\a=\sqrt[8]{9} \\log(a^b)=log(b^a)\\blog(a)=alog(b)\\\frac{b}{a}=\frac{log(b)}{log(a)}\\\frac{b}{a}=log_a(b)\\9=log_a(9a)\\a^9=9a\\a^8=9\\a=\sqrt[8]{9}](/latexrender/pictures/3948cfc71c8bd408dcf30bb2ada655d7.png)

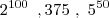
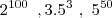
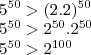
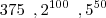



 , avisa que eu resolvo.
, avisa que eu resolvo.

