Gostaria de saber se estou resolvendo corretamente o exercício abaixo. Desde já agradeço a atenção de todos.
--> Calcule os valores de a e b para que o polinômio
 seja divisível por
seja divisível por  .
. -->
--> 
Se p(x) é de Grau 3 e é divisível por g(x) que é de Grau 2, o quociente q(x) é de Grau 1
 .
.Aplicando
 estou encontrando a equação:
estou encontrando a equação: 
Da igualdade dos polinômios estou encontrando:


Obrigado pela ajuda

Um abraço



 utilizado em
utilizado em  é utilizado em
é utilizado em  . Tanto que se você substituir os valores que você encontrou
. Tanto que se você substituir os valores que você encontrou  e
e  a divisão não dá exata.
a divisão não dá exata. por
por 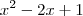 acho que é mais fácil não se confundir.
acho que é mais fácil não se confundir. terá que ser igual a 0 (para não haver resto).
terá que ser igual a 0 (para não haver resto).
 também será igual a 0, pelo mesmo motivo anterior.
também será igual a 0, pelo mesmo motivo anterior.


 e o resto não é nulo.
e o resto não é nulo.

 , avisa que eu resolvo.
, avisa que eu resolvo.

