beel escreveu:os pontos onde a derivada for zero ou nao existir será esses extremos certo?
Errado.
Se a derivada não existe no ponto, isso não significa necessariamente que há um mínimo ou máximo local naquele ponto.
Por exemplo, considere a função
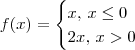
. Essa função não tem derivada em x = 0. Entretanto, nesse ponto não há máximo ou mínimo local. Faça um esboço do gráfico e verifique isso.
Por outro lado, se a primeira derivada é zero em um ponto, isso não significa necessariamente que há um mínimo ou máximo local naquele ponto.
Por exemplo, considere a função
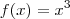
. Essa função tem primeira derivada igual a 0 em x = 0. Entretanto, nesse ponto não há máximo ou mínimo local. Faça um esboço do gráfico e verifique isso.
beel escreveu: derivada da função

será
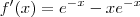
, assim o ponto onde ela será zero é 1.
Para achar os extremos:
(SABENDO QUE O DOMINIO DA FUNÇÃO É [0,5] )
f(0)= 0
f(5)= 0,032...
f(1)= 0.36...
posso afirmar que so existe um ponto de minimo?
Nesse caso sim.
Além disso, vale lembrar que as aproximações mais adequadas seriam:

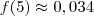
beel escreveu:...sei que o minimo global é zero... mas e o 0,0032?
O ponto x = 0,034 é um mínimo local.
beel escreveu:e posso afirmar que o ponto 1 é um máximo local?
Sim.
beel escreveu:...sei que 1 é um pt de maximo global...mas se é global tambem é local nao?
Todo ponto de máximo global é um ponto de máximo local, entretanto nem todo ponto de máximo local é um ponto de máximo global.
TheoFerraz escreveu:derivada que não existe mostra descontinuidade.
Errado.
Considere a função
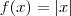
. Não existe derivada de f em x = 0, mas essa função é contínua em x = 0.
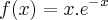 será
será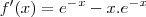 , assim o ponto onde ela será zero é 1.
, assim o ponto onde ela será zero é 1.

 mas isso voce ja sabia
mas isso voce ja sabia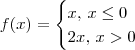 . Essa função não tem derivada em x = 0. Entretanto, nesse ponto não há máximo ou mínimo local. Faça um esboço do gráfico e verifique isso.
. Essa função não tem derivada em x = 0. Entretanto, nesse ponto não há máximo ou mínimo local. Faça um esboço do gráfico e verifique isso.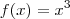 . Essa função tem primeira derivada igual a 0 em x = 0. Entretanto, nesse ponto não há máximo ou mínimo local. Faça um esboço do gráfico e verifique isso.
. Essa função tem primeira derivada igual a 0 em x = 0. Entretanto, nesse ponto não há máximo ou mínimo local. Faça um esboço do gráfico e verifique isso. será
será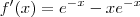 , assim o ponto onde ela será zero é 1.
, assim o ponto onde ela será zero é 1.
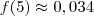
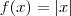 . Não existe derivada de f em x = 0, mas essa função é contínua em x = 0.
. Não existe derivada de f em x = 0, mas essa função é contínua em x = 0.