 por ihavenokia » Qua Out 26, 2011 15:12
por ihavenokia » Qua Out 26, 2011 15:12
Olá! Não estou percebendo como calcular os casos favoraveis deste problema
http://imageshack.us/photo/my-images/207/senome.png/os casos possiveis sao 12! ?
Obrigado pelas respostas.
-
ihavenokia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Out 26, 2011 15:07
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Neperiano » Qua Out 26, 2011 17:46
por Neperiano » Qua Out 26, 2011 17:46
Ola
Monte 12 lugares e va largando quantos podem sentar nesse lugar
12(qualquer um pode sentar na primera) x 6 (tenque ser uma rapariga ou um rapaz) x 5 (não pode repetir a mesma pessoa da esquerda)
E assim sucessivamente, não sei se ficou claro
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por jose henrique » Qua Out 26, 2011 21:05
por jose henrique » Qua Out 26, 2011 21:05
olá boa noite!!
trata de um exercício de permutação de elementos circulares, entretanto ele pede para que a resposta seja dada em porcentagem.
quantos eventos possíveis temos:
PC= (12-1)!= 39916800
Agora vamos ao evento que nos interessa que é quando os meninos estares entre as meninas, ou seja pessoas do mesmo sexo não podem sentar juntas.
são seis meninas e desta forma elas dentro dessa roda poderíam permutar:
PC= (6-1)!= 5! = 120
então poderíamos posicionar estas meninas nessa roda 120 maneiras diferentes.
como os meninos irão ficar entre as meninas então teríamos 6!= 720
pelo principio multiplicativo, teríamos: 120X720= 86400
bem o exercício pede que a resposta seja colocada em porcentagem, correto? então:
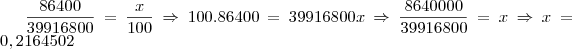
.
Você tem o gabarito da questão, confere aí se estar certo e depois posta. um abraço!!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Arranjo
por Pri Ferreira » Qua Mar 21, 2012 13:34
- 3 Respostas
- 2503 Exibições
- Última mensagem por LuizAquino

Seg Abr 09, 2012 23:30
Estatística
-
- Arranjo ! URGENTEEEEE
por my2009 » Qui Jun 03, 2010 19:08
- 3 Respostas
- 1609 Exibições
- Última mensagem por my2009

Sex Jun 04, 2010 23:07
Estatística
-
- Arranjo ou combinação?
por cristina » Sex Ago 27, 2010 11:41
- 3 Respostas
- 2322 Exibições
- Última mensagem por profmatematica

Sáb Ago 28, 2010 05:08
Estatística
-
- Arranjo ou Combinação?
por gustavowelp » Sex Nov 19, 2010 07:22
- 2 Respostas
- 1401 Exibições
- Última mensagem por gustavowelp

Sex Nov 19, 2010 13:36
Estatística
-
- Arranjo ou combinação??
por matpet92 » Dom Fev 12, 2012 12:40
- 2 Respostas
- 1446 Exibições
- Última mensagem por matpet92

Dom Fev 12, 2012 17:49
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




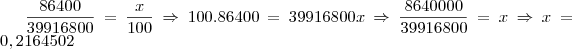 .
.