 por Raphael Feitas10 » Qua Out 26, 2011 00:56
por Raphael Feitas10 » Qua Out 26, 2011 00:56
A soma de três numeros e 39 e o produto 729. O segundo é a média proporcional ou geométrica entre os dois outros.Calcule os três numeros. R: 3,9,e 27
brother eu fiz ate aqui mais ñ conseguie fazer o resto e chagar a resposta... me ajuda aew por favor desde ja agradecido...
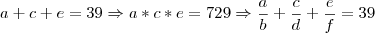
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Neperiano » Qua Out 26, 2011 14:11
por Neperiano » Qua Out 26, 2011 14:11
Ola
Você tem 3 incognitas então precisa de 3 equações
a+b+c=39
a.b.c=729
b=(a+c)/2
Agora é só isolar uma na outra que se acha todas
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qua Out 26, 2011 15:07
por MarceloFantini » Qua Out 26, 2011 15:07
Se ele disse que o segundo é média geométrica dos dois, então
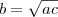
e não
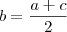
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Raphael Feitas10 » Qui Out 27, 2011 01:50
por Raphael Feitas10 » Qui Out 27, 2011 01:50
Marcelo como eu vou descobrir a e c se b é =
![\sqrt[]{ac} \sqrt[]{ac}](/latexrender/pictures/d442293c97b1d5e57228e1ad7444257a.png)
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Out 27, 2011 07:39
por MarceloFantini » Qui Out 27, 2011 07:39
Você tem três equações e três incógnitas, resolva e encontre-as.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Qui Out 27, 2011 14:11
por Neperiano » Qui Out 27, 2011 14:11
Ola
Lembre que raiz de 2 = 2^1/2
Você pode tirar elas da raiz se quiser fazendo isto aqui emcima
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qui Out 27, 2011 23:16
por MarceloFantini » Qui Out 27, 2011 23:16
Isso não muda nada, é só uma maneira diferente de escrever a mesma coisa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Proporção
por Roberta » Ter Jul 14, 2009 17:22
- 2 Respostas
- 3165 Exibições
- Última mensagem por Roberta

Ter Jul 14, 2009 19:53
Desafios Enviados
-
- PROPORÇÃO
por patriciagarciapoa » Qui Nov 05, 2009 16:37
- 1 Respostas
- 1776 Exibições
- Última mensagem por Lucio Carvalho

Qui Nov 05, 2009 17:14
Matemática Financeira
-
- Proporção
por Juliane » Seg Nov 22, 2010 10:32
- 2 Respostas
- 1955 Exibições
- Última mensagem por alexandre32100

Seg Nov 22, 2010 13:38
Álgebra Elementar
-
- Proporção
por Cristina Alves » Qui Fev 03, 2011 21:54
- 2 Respostas
- 2892 Exibições
- Última mensagem por Cristina Alves

Sex Fev 04, 2011 13:41
Álgebra Elementar
-
- Proporção 12
por Raphael Feitas10 » Sex Fev 18, 2011 00:06
- 1 Respostas
- 1446 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
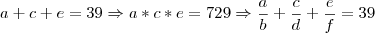

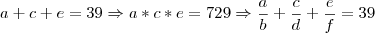


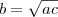 e não
e não 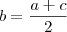 .
.

![\sqrt[]{ac} \sqrt[]{ac}](/latexrender/pictures/d442293c97b1d5e57228e1ad7444257a.png)




