 por Vininhuu » Sex Out 21, 2011 16:01
por Vininhuu » Sex Out 21, 2011 16:01
Eu precisava de ajuda nesse exercício:
"Seja

um triângulo. Mostre que:
a. Se

é um ponto interior de

, então
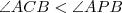
.
b. Se

é um ponto interior de

, então
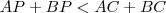
.
c. Se

é um ponto interior de

, então
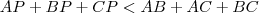
. E se

for exterior a

?"
Eu consegui resolver o item
a., mas não estou conseguindo resolver os outros...
É que eu precisava entregar a resposta desse exercício no domingo, dia 23/10/2011, mas não estou conseguindo resolver os itens
b. e
c.Eu estava pensando em tentar usar o Teorema de Pitágoras, ou alguma coisa assim, mas não consegui encontrar uma jeito de encaixar a soma dos lados no teorema.
Daí eu pensei em tentar provar por absurdo, primeiro mostrando que

não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que

não é possível. Coisa que não estou conseguindo fazer :S
Alguém poderia me ajudar, por favor ?
Agradeço !
-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Vininhuu » Sáb Out 22, 2011 17:07
por Vininhuu » Sáb Out 22, 2011 17:07
Vou postar aqui a resolução que eu encontrei do item
a.Usando a imagem abaixo para a melhor visualização da resposta,
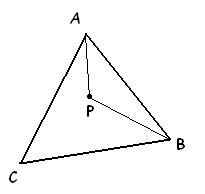
- Triângulo ABC.JPG (4.69 KiB) Exibido 2821 vezes
temos que:


O ponto

é interno, então
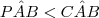
e







Mostrando que

.
Não sei se isso pode ajudar na resolução dos itens
b. e
c., mas espero que sim !
Muito obrigado por ao menos lerem

-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por dianabarreto » Sáb Out 22, 2011 20:34
por dianabarreto » Sáb Out 22, 2011 20:34
olá vininhu. Também sou do PIC e estou com problemas em resolver a parte

da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada:
Nesse mesmo triângulo que você desenhou, prolongue o seguimento
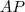
até o lado

num ponto
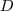
. Agora você irá analisar duas desigualdades:

e

. Some ambas e terá:

.
observe que

, entao vc terá:
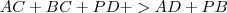
. Subtraia

de cada lado da desigualdade, ficando então com

c.q.d.
na letra c, você pode dizer que, com uma analise análoga a que foi feita no item b, tem que:

e
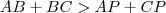
. Você soma as três desigualdades e obtêm que

. Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto

exterior a

.
Espero que com o que tenha dito você consiga resolvê-la e postar aqui, já que também preciso. [rs]
-
dianabarreto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Out 22, 2011 12:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Vininhuu » Dom Out 23, 2011 20:50
por Vininhuu » Dom Out 23, 2011 20:50
Diana, me desculpe, mas tentei de todo jeito reponder o resto do item c), mas não consegui :x
Eu inscrevi o

em uma circunferência para ver no que dava, tentei usar o Teorema de Pitágoras, tentei encontrar a área dos triângulos encontrados na imagem, mas não encontrei de jeito nenhum );
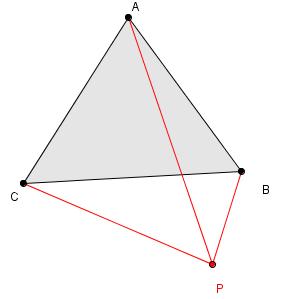
- Triângulo ABC + Ponto P exterior.JPG (7.05 KiB) Exibido 2792 vezes
Lhe agradeço muito por ter me ajudado nos itens b) e c), mas infelizmente, não pude te ajudar...
Mas, me passe seu msn para nós nos ajudarmos nas tarefas !
Vou conversar com meu P.O. sobre as tarefas do fórum, estão muito difíceis, e nenhuma das tarefas eu consegui responder sem a ajuda de alguém...
Eu só estava tendo a ajuda da minha professora da escola(que não é uma grande ajuda, rs), do meu P.O. (que não conseguiu me ajudar na tarefa 03), e do meu parceiro de encontros presenciais(que também tem um pouco de dificuldade para as respostas das tarefas).
Eu nem tento mais pedir ajuda para os meus colegas de fórum, pois os que conseguem responder são egoístas demais para me darem ao menos uma dica de como devo me posicionar perante ao exercício...
É difícil encontrar um alguém bondoso como você.
Agradeço-te novamente !
Meu msn: vini_demiciano_orsolon@hotmail.com
-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por dianabarreto » Dom Out 23, 2011 20:57
por dianabarreto » Dom Out 23, 2011 20:57
já te adicionei...
esperando aceitação XD dianabarreto@live.com
-
dianabarreto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Out 22, 2011 12:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6607 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- [Geometria] Triângulo ABC
por Vininhuu » Sex Out 21, 2011 14:28
- 0 Respostas
- 1891 Exibições
- Última mensagem por Vininhuu

Sex Out 21, 2011 14:28
Geometria
-
- Geometria.. triangulo
por juhfraga » Seg Mar 12, 2012 20:55
- 4 Respostas
- 5509 Exibições
- Última mensagem por emsbp

Qua Mar 14, 2012 12:12
Geometria Plana
-
- [Geometria] Área do triângulo
 por fernandocez » Sáb Out 20, 2012 14:47
por fernandocez » Sáb Out 20, 2012 14:47
- 2 Respostas
- 5570 Exibições
- Última mensagem por fernandocez

Sáb Out 20, 2012 21:13
Geometria Plana
-
- Geometria analitica - vertices do triangulo
por Dayannearaujo » Qui Abr 19, 2012 17:21
- 1 Respostas
- 2329 Exibições
- Última mensagem por LuizAquino

Sex Abr 20, 2012 00:07
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 um triângulo. Mostre que:
um triângulo. Mostre que: é um ponto interior de
é um ponto interior de  , então
, então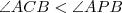 .
. é um ponto interior de
é um ponto interior de  , então
, então 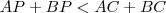 .
. é um ponto interior de
é um ponto interior de  , então
, então 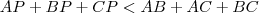 . E se
. E se  for exterior a
for exterior a  ?"
?" não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que
não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que  não é possível. Coisa que não estou conseguindo fazer :S
não é possível. Coisa que não estou conseguindo fazer :S



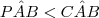 e
e 





 .
.
 da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada:
da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada: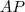 até o lado
até o lado  num ponto
num ponto 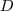 . Agora você irá analisar duas desigualdades:
. Agora você irá analisar duas desigualdades: e
e  . Some ambas e terá:
. Some ambas e terá:  .
. , entao vc terá:
, entao vc terá: 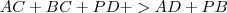 . Subtraia
. Subtraia  de cada lado da desigualdade, ficando então com
de cada lado da desigualdade, ficando então com 
 e
e 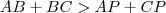 . Você soma as três desigualdades e obtêm que
. Você soma as três desigualdades e obtêm que  . Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto
. Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto  .
.