 por Vininhuu » Sex Out 21, 2011 16:01
por Vininhuu » Sex Out 21, 2011 16:01
Eu precisava de ajuda nesse exercício:
"Seja

um triângulo. Mostre que:
a. Se

é um ponto interior de

, então
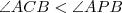
.
b. Se

é um ponto interior de

, então
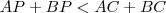
.
c. Se

é um ponto interior de

, então
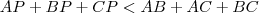
. E se

for exterior a

?"
Eu consegui resolver o item
a., mas não estou conseguindo resolver os outros...
É que eu precisava entregar a resposta desse exercício no domingo, dia 23/10/2011, mas não estou conseguindo resolver os itens
b. e
c.Eu estava pensando em tentar usar o Teorema de Pitágoras, ou alguma coisa assim, mas não consegui encontrar uma jeito de encaixar a soma dos lados no teorema.
Daí eu pensei em tentar provar por absurdo, primeiro mostrando que

não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que

não é possível. Coisa que não estou conseguindo fazer :S
Alguém poderia me ajudar, por favor ?
Agradeço !
-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Vininhuu » Sáb Out 22, 2011 17:07
por Vininhuu » Sáb Out 22, 2011 17:07
Vou postar aqui a resolução que eu encontrei do item
a.Usando a imagem abaixo para a melhor visualização da resposta,
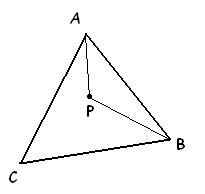
- Triângulo ABC.JPG (4.69 KiB) Exibido 2827 vezes
temos que:


O ponto

é interno, então
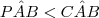
e







Mostrando que

.
Não sei se isso pode ajudar na resolução dos itens
b. e
c., mas espero que sim !
Muito obrigado por ao menos lerem

-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por dianabarreto » Sáb Out 22, 2011 20:34
por dianabarreto » Sáb Out 22, 2011 20:34
olá vininhu. Também sou do PIC e estou com problemas em resolver a parte

da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada:
Nesse mesmo triângulo que você desenhou, prolongue o seguimento
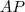
até o lado

num ponto
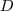
. Agora você irá analisar duas desigualdades:

e

. Some ambas e terá:

.
observe que

, entao vc terá:
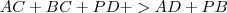
. Subtraia

de cada lado da desigualdade, ficando então com

c.q.d.
na letra c, você pode dizer que, com uma analise análoga a que foi feita no item b, tem que:

e
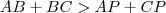
. Você soma as três desigualdades e obtêm que

. Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto

exterior a

.
Espero que com o que tenha dito você consiga resolvê-la e postar aqui, já que também preciso. [rs]
-
dianabarreto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Out 22, 2011 12:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Vininhuu » Dom Out 23, 2011 20:50
por Vininhuu » Dom Out 23, 2011 20:50
Diana, me desculpe, mas tentei de todo jeito reponder o resto do item c), mas não consegui :x
Eu inscrevi o

em uma circunferência para ver no que dava, tentei usar o Teorema de Pitágoras, tentei encontrar a área dos triângulos encontrados na imagem, mas não encontrei de jeito nenhum );
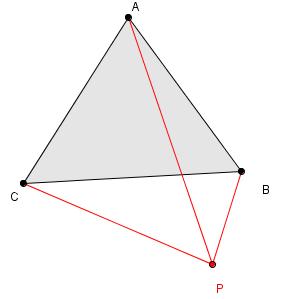
- Triângulo ABC + Ponto P exterior.JPG (7.05 KiB) Exibido 2798 vezes
Lhe agradeço muito por ter me ajudado nos itens b) e c), mas infelizmente, não pude te ajudar...
Mas, me passe seu msn para nós nos ajudarmos nas tarefas !
Vou conversar com meu P.O. sobre as tarefas do fórum, estão muito difíceis, e nenhuma das tarefas eu consegui responder sem a ajuda de alguém...
Eu só estava tendo a ajuda da minha professora da escola(que não é uma grande ajuda, rs), do meu P.O. (que não conseguiu me ajudar na tarefa 03), e do meu parceiro de encontros presenciais(que também tem um pouco de dificuldade para as respostas das tarefas).
Eu nem tento mais pedir ajuda para os meus colegas de fórum, pois os que conseguem responder são egoístas demais para me darem ao menos uma dica de como devo me posicionar perante ao exercício...
É difícil encontrar um alguém bondoso como você.
Agradeço-te novamente !
Meu msn: vini_demiciano_orsolon@hotmail.com
-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por dianabarreto » Dom Out 23, 2011 20:57
por dianabarreto » Dom Out 23, 2011 20:57
já te adicionei...
esperando aceitação XD dianabarreto@live.com
-
dianabarreto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Out 22, 2011 12:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6607 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- [Geometria] Triângulo ABC
por Vininhuu » Sex Out 21, 2011 14:28
- 0 Respostas
- 1891 Exibições
- Última mensagem por Vininhuu

Sex Out 21, 2011 14:28
Geometria
-
- Geometria.. triangulo
por juhfraga » Seg Mar 12, 2012 20:55
- 4 Respostas
- 5517 Exibições
- Última mensagem por emsbp

Qua Mar 14, 2012 12:12
Geometria Plana
-
- [Geometria] Área do triângulo
 por fernandocez » Sáb Out 20, 2012 14:47
por fernandocez » Sáb Out 20, 2012 14:47
- 2 Respostas
- 5572 Exibições
- Última mensagem por fernandocez

Sáb Out 20, 2012 21:13
Geometria Plana
-
- Geometria analitica - vertices do triangulo
por Dayannearaujo » Qui Abr 19, 2012 17:21
- 1 Respostas
- 2334 Exibições
- Última mensagem por LuizAquino

Sex Abr 20, 2012 00:07
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 um triângulo. Mostre que:
um triângulo. Mostre que: é um ponto interior de
é um ponto interior de  , então
, então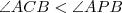 .
. é um ponto interior de
é um ponto interior de  , então
, então 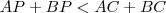 .
. é um ponto interior de
é um ponto interior de  , então
, então 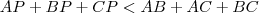 . E se
. E se  for exterior a
for exterior a  ?"
?" não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que
não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que  não é possível. Coisa que não estou conseguindo fazer :S
não é possível. Coisa que não estou conseguindo fazer :S



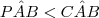 e
e 





 .
.
 da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada:
da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada: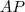 até o lado
até o lado  num ponto
num ponto 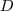 . Agora você irá analisar duas desigualdades:
. Agora você irá analisar duas desigualdades: e
e  . Some ambas e terá:
. Some ambas e terá:  .
. , entao vc terá:
, entao vc terá: 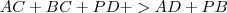 . Subtraia
. Subtraia  de cada lado da desigualdade, ficando então com
de cada lado da desigualdade, ficando então com 
 e
e 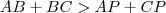 . Você soma as três desigualdades e obtêm que
. Você soma as três desigualdades e obtêm que  . Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto
. Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto  .
.  } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: