 por Fabio010 » Sex Out 21, 2011 20:19
por Fabio010 » Sex Out 21, 2011 20:19
Olá pessoal
Como podem ver sou novo no forúm. Penso que estou a criar um tópico na secção correcta.
Bem eu tenho aqui uma dúvida para resolver o domínio desta função.
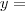

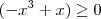

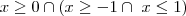
Domínio=
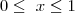
Eu resolvi assim. Mas pelas soluções, sei que está incorrecto. Pois devia dar
![]-\infty, -1] ]-\infty, -1]](/latexrender/pictures/a635591009712a8de400951e175a84ab.png)
,
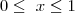
Alguém me ajuda para eu saber qual foi o procedimento errado?
-
Fabio010
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por DanielFerreira » Sáb Mar 03, 2012 21:59
por DanielFerreira » Sáb Mar 03, 2012 21:59
Fabio010 escreveu:Olá pessoal
Como podem ver sou novo no forúm. Penso que estou a criar um tópico na secção correcta.
Bem eu tenho aqui uma dúvida para resolver o domínio desta função.
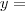

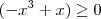

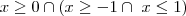
Domínio=
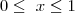
Eu resolvi assim. Mas pelas soluções, sei que está incorrecto. Pois devia dar
![]-\infty, -1] ]-\infty, -1]](/latexrender/pictures/a635591009712a8de400951e175a84ab.png)
,
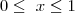
Alguém me ajuda para eu saber qual foi o procedimento errado?
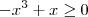
 Condição I:
Condição I: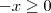
======> multiplicando por (- 1
 Condição II:
Condição II: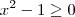
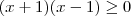
Tabela...
___+__________+_____(0)___-____________-____
___+____(-1)___-__________-______(+1)___+____
___
+____(-1)___-_____(0)___
+_____(+1)___-_____

ou
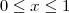
![]-\infty, -1] ]-\infty, -1]](/latexrender/pictures/a635591009712a8de400951e175a84ab.png)
,
![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3260 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2891 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1776 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5181 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
-
- Domínio de uma função
por Jonatan » Qui Jul 29, 2010 15:46
- 0 Respostas
- 1870 Exibições
- Última mensagem por Jonatan

Qui Jul 29, 2010 15:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
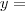

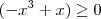

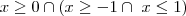
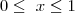
![]-\infty, -1] ]-\infty, -1]](/latexrender/pictures/a635591009712a8de400951e175a84ab.png) ,
, 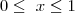


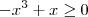

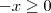 ======> multiplicando por (- 1
======> multiplicando por (- 1
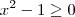
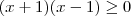
 ou
ou 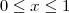
![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)


 .
.
 :
: