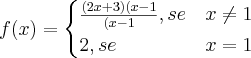
A resolução seria:
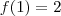
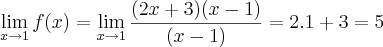
A função é descontínua no ponto x=1, porque em
 , o resultado teria que ser também 2, como em x=1, correto?
, o resultado teria que ser também 2, como em x=1, correto?
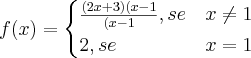
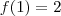
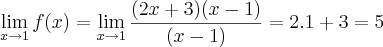
 , o resultado teria que ser também 2, como em x=1, correto?
, o resultado teria que ser também 2, como em x=1, correto?



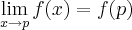
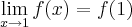

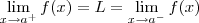
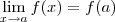 na função
na função 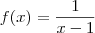 no ponto 1.. Você verá que ela é contínua em todo o domínio menos no ponto 1, pois seus limites laterais são diferentes...
no ponto 1.. Você verá que ela é contínua em todo o domínio menos no ponto 1, pois seus limites laterais são diferentes... a sua função apresenta outra "cara", logo, para verificar se ela é contínua você teria que fazer o teste dos limites laterais, assim você poderá dizer se a função é contínua em todo o seu domínio (mesmo que a f(1) seja diferente do valor encontrado no limite).
a sua função apresenta outra "cara", logo, para verificar se ela é contínua você teria que fazer o teste dos limites laterais, assim você poderá dizer se a função é contínua em todo o seu domínio (mesmo que a f(1) seja diferente do valor encontrado no limite). "..
"..

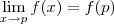 .
.


MarceloFantini escreveu:A função é descontínua. Você está errando Renato. É verdade que não necessariamente o limite é o valor da função no ponto (pois ela pode nem estar definida), mas ela será contínua se e somente se o limite for igual ao valor da função no ponto, ou seja, sempre que.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.