O raio de um cone circular reto aumenta 1,8 pol/s mas a altura decresce a taxa de 2,5 pol/s. Qual a taxa de variação do volume do cone, quando o raio vale 120 pol e altura h = 140 pol?
Eu li a matéria no Stewart mas não entendi muito bem. Eu simplesmente calculei as derivadas parciais em relação ao volume, no ponto (120,140). Está certo resolver desse jeito?


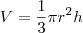 .
.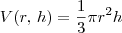 .
.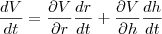
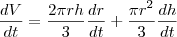
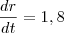 ,
, 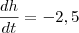 ,
,  e
e 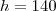 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)