Sabe-se que uma alimentação diária equilibrada em vitaminas deve constar de 91 unidades de vitamina A, 54 unidades de vitamina B, 34 unidades de vitamina C e 31 unidades de vitamina D.
Com o objetivo de descobrir como deverá ser uma refeição equilibrada, foram estudados cinco alimentos. Fixada a mesma quantidade (1 g) de cada alimento,determinou-se que:
i) O alimento I tem 1 unidade de vitamina A, 10 unidades de vitamina B, 1 unidade de vitamina C e 2 unidades de vitamina D.
ii) O alimento II tem 9 unidades de vitamina A, 1 unidade de vitamina B, 0 unidade de vitamina C e 1 unidade de vitamina D.
iii) O alimento III tem 2 unidades de A, 2 unidades de B, 5 unidades de C e 1 unidade de D.
iv) O alimento IV tem 1 unidade de A, 1 unidade de B, 1 unidade de C e 2 unidades de D.
Quantas gramas de cada um dos alimentos I, II, III e IV devemos ingerir diariamente para que nossa alimentação seja equilibrada?
COMECEI MONTANDO A MATRIZ QUE FICOU DA SEGUINTE FORMA:
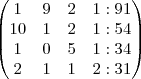
AGORA PRECISO ESCALONAR E NÃO SEI, ALGUÉM PODERIA ME AJUDAR, SE POSSÍVEL EXPLICANDO PARA QUE EU CONSIGA ENTENDER ESTE PROCESSO?
Obrigada
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.