Mostre, usando o teorema do confronto, que, se
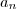 ->0, então,
->0, então, 
Conclua então que, se
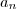 ->0, então
->0, então 

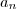 ->0, então,
->0, então, 
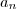 ->0, então
->0, então 

 . Aplicando o teorema do confronto, o limite da esquerda vai para zero, o limite da direita vai para zero, e portanto o limite
. Aplicando o teorema do confronto, o limite da esquerda vai para zero, o limite da direita vai para zero, e portanto o limite  .
.

MarceloFantini escreveu:Note que podemos afirmar que. Aplicando o teorema do confronto, o limite da esquerda vai para zero, o limite da direita vai para zero, e portanto o limite
.
 ?
?
 é não decrescente, e o único intervalo onde isto poderia dar problema é
é não decrescente, e o único intervalo onde isto poderia dar problema é  .
.

 .
.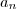 é que essa sequência tende a zero, quando n tende ao infinito. Mas como isso implica que seu módulo é sempre maior que o módulo de
é que essa sequência tende a zero, quando n tende ao infinito. Mas como isso implica que seu módulo é sempre maior que o módulo de  ? Isso vem de alguma prova geométrica?
? Isso vem de alguma prova geométrica?
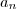 :
:
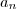 :
:


 (já tomando isso com verdadeiro). E, para mostrar que
(já tomando isso com verdadeiro). E, para mostrar que  (que é a outra parte do exercício), é preciso utilizar
(que é a outra parte do exercício), é preciso utilizar 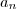 ->0
->0 .
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)