 por matmatco » Qui Set 01, 2011 11:04
por matmatco » Qui Set 01, 2011 11:04
olá, estou com dificuldade em resolver esse limite:
 ( lembrando o x está tendendo a zero)
( lembrando o x está tendendo a zero)tentei dividir tudo por senax+senbx mas não consegui, tentei fazendo

mas não consegui sair disso alguem me explique como resolver obrigado.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por LuizAquino » Qui Set 01, 2011 12:34
por LuizAquino » Qui Set 01, 2011 12:34
DicasEu presumo que a ideia seja resolver esse limite
sem usar a Regra de L'Hospital. Para isso, comece usando as sugestões abaixo.
No numerador escreva

.
Já no denominador, use a identidade trigonométrica

.
Em seguida, tente dividir o numerador e o denominador por uma expressão de modo a fazer aparecer o limite trigonométrico fundamental.
Além disso, veja as ideias discutidas no tópico abaixo. Você vai precisar aplicar uma estratégia semelhante.
[limite] Ajuda com limite!viewtopic.php?f=120&t=5769#p19973Tente terminar o exercício. Se você não conseguir, poste aqui até onde você conseguiu desenvolver com essas dicas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por matmatco » Qui Set 01, 2011 16:12
por matmatco » Qui Set 01, 2011 16:12
usei a identidade e encontrei uma resposta igual a 2, ai voltando ao limite ficou
x está tendendo a zero
=

=

ai fiquei com duvida se eu posso fazer esses dois ultimos passos ...
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por LuizAquino » Qui Set 01, 2011 17:13
por LuizAquino » Qui Set 01, 2011 17:13
matmatco escreveu:usei a identidade e encontrei uma resposta igual a 2, ai voltando ao limite ficou

Não fica somente isso.
Nós temos que:
![\lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}](/latexrender/pictures/e7c8ff071ee7b218a291aaf66a12f15c.png)
Dividindo o numerador e o denominador por

(lembrando que devemos ter

), ficamos com
![\lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\frac{(a-b)x}{2}}}{\frac{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}{\frac{(a-b)x}{2}}} = \frac{1}{a-b} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{x} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\frac{(a-b)x}{2}}}{\frac{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}{\frac{(a-b)x}{2}}} = \frac{1}{a-b} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{x}](/latexrender/pictures/2d09537aeb33be1ee013e4e7d41ad30f.png)
Podemos então escrever que:

Para continuar a resolução, veja a estratégia usada no
tópico que indiquei acima.
Observação 1Para inserir o "x tendendo a zero" no limite, use o comando LaTeX:
- Código: Selecionar todos
x \to 0
O resultado desse comando é:
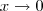
.
Ou seja, para ter algo como
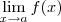
, usamos o comando LaTeX:
- Código: Selecionar todos
\lim_{x\to a} f(x)
Observação 2Vale lembrar também que
é falsa a equação:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Sex Set 02, 2011 00:34
por nietzsche » Sex Set 02, 2011 00:34
luiz,
se a= 0 a observação 2 é correta.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Set 02, 2011 08:30
por LuizAquino » Sex Set 02, 2011 08:30
nietzsche escreveu:luiz,
se a= 0 a observação 2 é correta.
De fato. Mas vale lembrar que apenas para x diferente de zero. Note que se a = x = 0 teríamos uma operação inválida no segundo membro.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por matmatco » Qui Set 08, 2011 10:19
por matmatco » Qui Set 08, 2011 10:19
olá,
encontrei uma maneira mais facil e rapida de resolver , se dividir tudo por x encontramos direto a parte

ae já está resolvido o problema
obs: postarei a resolução completa na proxima
obrigado pela ajuda abraços
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite fundamental]
por TheKyabu » Qui Out 25, 2012 18:33
- 1 Respostas
- 1725 Exibições
- Última mensagem por TheKyabu

Qui Out 25, 2012 18:50
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental
por Julia Maia » Seg Abr 25, 2016 14:17
- 0 Respostas
- 2087 Exibições
- Última mensagem por Julia Maia

Seg Abr 25, 2016 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Limite Fundamental
por Everton Pire Souza » Dom Abr 30, 2017 23:58
- 0 Respostas
- 2968 Exibições
- Última mensagem por Everton Pire Souza

Dom Abr 30, 2017 23:58
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE]LIMITE FUNDAMENTAL EXPONENCIAL
por beel » Sáb Set 03, 2011 22:11
- 3 Respostas
- 2391 Exibições
- Última mensagem por beel

Dom Set 04, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental Trigonometrico
por fabioengcomp » Sáb Abr 16, 2011 12:31
- 2 Respostas
- 2201 Exibições
- Última mensagem por Molina

Sáb Abr 16, 2011 20:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ( lembrando o x está tendendo a zero)
( lembrando o x está tendendo a zero) mas não consegui sair disso alguem me explique como resolver obrigado.
mas não consegui sair disso alguem me explique como resolver obrigado.
 ( lembrando o x está tendendo a zero)
( lembrando o x está tendendo a zero) mas não consegui sair disso alguem me explique como resolver obrigado.
mas não consegui sair disso alguem me explique como resolver obrigado.
 .
. .
.
 =
=  =
= 


![\lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}](/latexrender/pictures/e7c8ff071ee7b218a291aaf66a12f15c.png)
 (lembrando que devemos ter
(lembrando que devemos ter  ), ficamos com
), ficamos com![\lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\frac{(a-b)x}{2}}}{\frac{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}{\frac{(a-b)x}{2}}} = \frac{1}{a-b} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{x} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\textrm{sen}\,ax - \,\textrm{sen}\,bx} = \lim_{x\to 0}\frac{\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{\frac{(a-b)x}{2}}}{\frac{2\,\textrm{sen}\,\left[\frac{(a-b)x}{2}\right]\cos\left[\frac{(a+b)x}{2}\right]}{\frac{(a-b)x}{2}}} = \frac{1}{a-b} \lim_{x\to 0}\frac{({e}^{ax} - 1) - ({e}^{bx} - 1)}{x}](/latexrender/pictures/2d09537aeb33be1ee013e4e7d41ad30f.png)

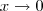 .
.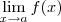 , usamos o comando LaTeX:
, usamos o comando LaTeX: .
.


 ae já está resolvido o problema
ae já está resolvido o problema 


 , avisa que eu resolvo.
, avisa que eu resolvo.

