 por claudiospj » Sáb Ago 06, 2011 16:35
por claudiospj » Sáb Ago 06, 2011 16:35
Uma questão que já tem um tempo que tento responder:
Em certa comunidade há indivíduos de três raças: Braca, Preta e Amarela. sabendo que 70% são brancos e 210 não são Pretos e 50% são amarela. Pergunta-se:
a) Quantos indivíduos tem a comunidade?
b) Quantos são os indivíduos amarelo?
R- a) 560, b)280
-
claudiospj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 06, 2011 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por Molina » Sáb Ago 06, 2011 17:03
por Molina » Sáb Ago 06, 2011 17:03
Boa tarde, Claudio.
claudiospj escreveu:Uma questão que já tem um tempo que tento responder:
Em certa comunidade há indivíduos de três raças: Braca, Preta e Amarela. sabendo que 70% são brancos e 210 não são Pretos e 50% são amarela. Pergunta-se:
a) Quantos indivíduos tem a comunidade?
b) Quantos são os indivíduos amarelo?
R- a) 560, b)280
De onde você tirou esta questão? Deve haver algum erro de digitação no enunciado, pois se 70% são brancos e 50% são amarelos já temos um número maior do que suportado pelo conjunto de todas as pessoas:
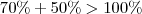
.
Aguardo sua confirmação dos valores.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por claudiospj » Sáb Ago 06, 2011 17:13
por claudiospj » Sáb Ago 06, 2011 17:13
É isso mesmo, eu retirei do livro fundamentos de matemática elementar 1 (Gelson Iezzi, Carlos Murakami)
questão A48
esse é um livro de Ensino médio
-
claudiospj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 06, 2011 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por claudiospj » Sáb Ago 06, 2011 19:59
por claudiospj » Sáb Ago 06, 2011 19:59
alguem ajuda ai!
-
claudiospj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 06, 2011 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por MarceloFantini » Sáb Ago 06, 2011 23:36
por MarceloFantini » Sáb Ago 06, 2011 23:36
O problema é que com essas porcentagens o problema assume que existe interseção entre os conjuntos: branco e preto ou preto e amarelo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por claudiospj » Dom Ago 07, 2011 00:07
por claudiospj » Dom Ago 07, 2011 00:07
pode ser que sim, pode ser que não.
-
claudiospj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 06, 2011 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por MarceloFantini » Dom Ago 07, 2011 00:19
por MarceloFantini » Dom Ago 07, 2011 00:19
Seja n o número de pessoas na comunidade. Sabemos que

. O enunciado diz que
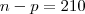
e
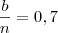
e
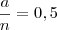
. Então

e dividindo tudo por n temos
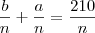
, o que implica
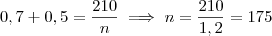
. Veja os problemas que isto acarreta:
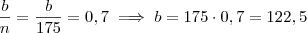
e
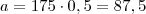
! Não podemos ter "meio indivíduo". Será que existe a suposição de miscigenação? Não creio que seja isto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por claudiospj » Dom Ago 07, 2011 03:59
por claudiospj » Dom Ago 07, 2011 03:59
realmente a questão só diz isso.
-
claudiospj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 06, 2011 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6421 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4730 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7959 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11208 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


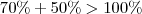 .
.

 . O enunciado diz que
. O enunciado diz que 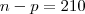 e
e 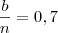 e
e 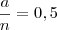 . Então
. Então  e dividindo tudo por n temos
e dividindo tudo por n temos 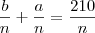 , o que implica
, o que implica 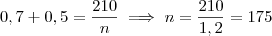 . Veja os problemas que isto acarreta:
. Veja os problemas que isto acarreta: 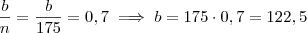 e
e 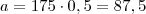 ! Não podemos ter "meio indivíduo". Será que existe a suposição de miscigenação? Não creio que seja isto.
! Não podemos ter "meio indivíduo". Será que existe a suposição de miscigenação? Não creio que seja isto.