 por Claudin » Sex Ago 05, 2011 03:02
por Claudin » Sex Ago 05, 2011 03:02
Não consigo encontrar uma maneira mais fácil de fatorar, tais expressões, alguém poderia passar algumas dicas. E peço também para que alguém verifique se a resolução está correta. (O exercício pede para que simplifique o máximo possível).
Deduzindo algumas raízes e utilizando o
WolframAlpha, gostaria de saber se tem algumas dicas para fatoração de polinômios.
Resolução:
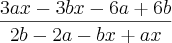
Dividindo o numerador por 3 obtive:
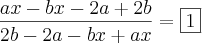
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Sex Ago 05, 2011 12:20
por FilipeCaceres » Sex Ago 05, 2011 12:20
Claudin escreveu:Não consigo encontrar uma maneira mais fácil de fatorar, tais expressões, alguém poderia passar algumas dicas.
E peço também para que alguém verifique se a resolução está correta. (O exercício pede para que simplifique o máximo possível).
Deduzindo algumas raízes e utilizando o
WolframAlpha, gostaria de saber se tem algumas dicas para fatoração de polinômios.
Resolução:
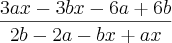
Dividindo o numerador por 3 obtive:
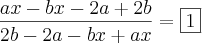
Se você realmente usar o
WolframAlpha verá que a sua solução está errada, veja
- Código: Selecionar todos
http://www.wolframalpha.com/input/?i=\frac{3ax-3bx-6a%2B6b}{2b-2a-bx%2Bax}
Temos,
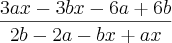
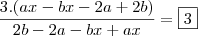
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8926 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3262 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8830 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2547 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 4087 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
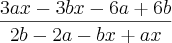
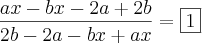

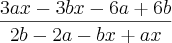
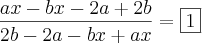

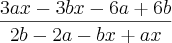
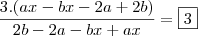

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
