 por Anderson Carvalho » Qua Jul 27, 2011 19:23
por Anderson Carvalho » Qua Jul 27, 2011 19:23
Olá pessoal, estava tentando resolver essa questao de geometria , mas nao to conseguindo.Queria alguma ajuda, grato!!!
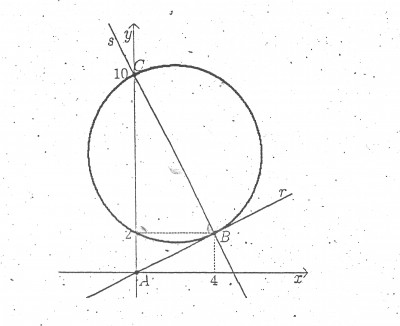
O enunciado é o seguinte: Na figura abaixo considere o circulo que contem os pontos B(4,2) , C(0,10) e D(0,2), a reta r é tangente ao circulo em B e s é uma reta que passa por B e C. Qual a área da regiao interna ao circulo limitada entre o eixo y e a reta s?
A resposta é 8+20arcsen(raiz quadrada de 5 sobre 5)
Chamei o centro de E
Tentei da seguinte maneira : com as informaçoes da questao conclui que a reta s(que passa por C e B) contem o centro E da circuferencia que é (2,6). O raio calculei e obtive 2raiz de 5 sobre 5. Resumindo a area pedida é a area do triangulo BCD + area do segmento circular BD. Pra calcular essa area do segmento circular nao to conseguindo, tentei achar a area do setor circular BD - area do triangulo BDE. As areas dos triangulos sao faceis ja achei , sao: triangulo BCD=16 e area do triangulo BDE=8. Tive a ideia tb de calcular a area do segmento integrando de 2 a 4 entre a reta y=2 e a equaçao da circunferencia mas nao to conseguindo, se alguem enxergar algum caminho gostaria de saber
Valeu, conto com vcs
- imagem de circunferencia
Editado pela última vez por
Anderson Carvalho em Qua Jul 27, 2011 21:00, em um total de 1 vez.
-
Anderson Carvalho
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 26, 2011 23:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matematica
- Andamento: formado
 por Molina » Qua Jul 27, 2011 20:08
por Molina » Qua Jul 27, 2011 20:08
Boa tarde.
Onde está a figura?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Anderson Carvalho » Qua Jul 27, 2011 20:12
por Anderson Carvalho » Qua Jul 27, 2011 20:12
Nao to conseguindo colocar como anexo, como q eu faço?
-
Anderson Carvalho
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 26, 2011 23:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matematica
- Andamento: formado
 por Molina » Qua Jul 27, 2011 20:26
por Molina » Qua Jul 27, 2011 20:26
Anderson Carvalho escreveu:Nao to conseguindo colocar como anexo, como q eu faço?
Você pode usar o
ImageShack para armazenar sua imagem e repassar o endereço da imagem.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Anderson Carvalho » Qua Jul 27, 2011 21:01
por Anderson Carvalho » Qua Jul 27, 2011 21:01
ta ai a figura
-
Anderson Carvalho
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 26, 2011 23:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matematica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral - Cálculo de áreas
por pinkfluor » Qui Jul 21, 2011 11:38
- 3 Respostas
- 2934 Exibições
- Última mensagem por pinkfluor

Qui Jul 21, 2011 17:21
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Cálculo de áreas
 por AlbertoAM » Ter Jun 28, 2011 00:25
por AlbertoAM » Ter Jun 28, 2011 00:25
- 5 Respostas
- 6612 Exibições
- Última mensagem por AlbertoAM

Qua Jun 29, 2011 20:44
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de áreas por integrais
 por Faby » Seg Set 19, 2011 10:50
por Faby » Seg Set 19, 2011 10:50
- 9 Respostas
- 6362 Exibições
- Última mensagem por Faby

Qui Set 22, 2011 00:41
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Áreas utilizando integrais
por Rambox » Ter Jun 14, 2011 14:38
- 2 Respostas
- 2227 Exibições
- Última mensagem por Rambox

Ter Jun 14, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Cálculo de Áreas - Guidorizzi
por Lennon » Sáb Jun 08, 2013 02:24
- 2 Respostas
- 2841 Exibições
- Última mensagem por Lennon

Dom Jun 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
