 por Neperiano » Qui Fev 12, 2009 11:15
por Neperiano » Qui Fev 12, 2009 11:15
Ola
Essa é uma duvida de uma pessoa no chat.
Eu mais ou menos acho que sei, mas é que não aprendi ainda, dai naum tenho certeza.
Bom vamos a ela.
Um cubo tem 1,00m .calcule sua area total com aresta2?
Ele respondeu p=1*1=12.
Aproveitando q ele quer saber se esta certo, eu gostaria de saber como se faz pra chegar lah, pq quero aprender tambem.
Obrigado
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Qui Fev 12, 2009 18:50
por Molina » Qui Fev 12, 2009 18:50
Boa tarde, Maligno.
Obrigado por colocar aqui dúvidas de pessoas do chat.
Mas não entendi muito bem o enunciado:
Um cubo tem 1,00m .calcule sua area total com aresta2?
seria 1,00m³ ? ou tem arestas de 1 metro? acho que faltou alguma coisa ali.
outra duvida o que seria
aresta2?
Ele respondeu p=1*1=12.
1 vezes 1 = 12?
Tente esclarecer essas minhas dúvidas que assim que possível eu coloco o resultado.
Abraços

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Qui Fev 12, 2009 20:09
por Neperiano » Qui Fev 12, 2009 20:09
Ola
Poise eu tambem não sei, quando o caras falou eu tambem não entendi, vamos fazer de uma forma se não for essa o cara vai ver e vai dizer como é.
Quanto a primeira acredito que seja 1.00m3 e quanto aresta 2, deve ser soh aresta.
Quanto a seguna eh sim 1x1=12.
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Qui Fev 12, 2009 20:48
por Molina » Qui Fev 12, 2009 20:48
Nossa! Acho que está mais difícil decifrar o problema do que a resposta dele.
Eu acho que ao inves de 1x1=12 ele queria dizer 1x12=12,
pois o cubo tem 12 arestas.
Entendeu?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sex Fev 13, 2009 10:30
por Neperiano » Sex Fev 13, 2009 10:30
Ola
Bom, pode ser que a resposta dele esteja errada. Tah se um cubo tem 12 Aresta entaum é soh dividir o 1,00 por 12?
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Fev 13, 2009 13:36
por Molina » Sex Fev 13, 2009 13:36
Maligno escreveu:Ola
Bom, pode ser que a resposta dele esteja errada. Tah se um cubo tem 12 Aresta entaum é soh dividir o 1,00 por 12?
Abraços
Boa trade.
Não, não é isso.
A fórmula para saber o volume de um cubo é

. Se ele está dizendo que o cubo tem volume igual a 1,00m³, ou seja:

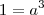
![\sqrt[3]{1}=a \sqrt[3]{1}=a](/latexrender/pictures/f055adaae6f1c2eb59bc75f743ce422c.png)

Ou seja,
a que neste caso representa a Aresta é igual a 1,00m quando se tem um cubo com volume de 1,00m³
Ficou claro?
Só nao sei se era isso que ele queria no problema.
Abraços

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sex Fev 13, 2009 13:57
por Neperiano » Sex Fev 13, 2009 13:57
Ola
Sim a fórmula eu ja sabia, trabalhei essa formula em fisica, em dilatação Térmica, mas tambem naum sei se era isso, vamos esperar ele falar alguma coisa se é isso, se não disser nada deve ser.
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cubo
 por camilalindynha » Ter Dez 11, 2007 18:56
por camilalindynha » Ter Dez 11, 2007 18:56
- 1 Respostas
- 6821 Exibições
- Última mensagem por admin

Ter Dez 11, 2007 20:05
Geometria Espacial
-
- Cubo (FEI - SP)
 por Ananda » Qua Fev 27, 2008 16:05
por Ananda » Qua Fev 27, 2008 16:05
- 3 Respostas
- 5126 Exibições
- Última mensagem por agp16

Dom Nov 08, 2009 21:42
Geometria Espacial
-
- CUBO
por Thassya » Seg Out 11, 2010 21:46
- 9 Respostas
- 5280 Exibições
- Última mensagem por MarceloFantini

Qua Out 20, 2010 21:48
Geometria Plana
-
- Cubo
 por Pri Ferreira » Qua Mar 21, 2012 14:17
por Pri Ferreira » Qua Mar 21, 2012 14:17
- 1 Respostas
- 1645 Exibições
- Última mensagem por LuizAquino

Ter Mar 27, 2012 18:05
Geometria Espacial
-
- cubo
por von grap » Qua Mai 09, 2012 18:36
- 0 Respostas
- 1929 Exibições
- Última mensagem por von grap

Qua Mai 09, 2012 18:36
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 . Se ele está dizendo que o cubo tem volume igual a 1,00m³, ou seja:
. Se ele está dizendo que o cubo tem volume igual a 1,00m³, ou seja: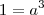
![\sqrt[3]{1}=a \sqrt[3]{1}=a](/latexrender/pictures/f055adaae6f1c2eb59bc75f743ce422c.png)


 .
.
 :
: