 por crfsatisfaction » Seg Jul 25, 2011 00:15
por crfsatisfaction » Seg Jul 25, 2011 00:15
Estou estudando para um concurso no fim do ano e me deparei com um problema que não consegui resolver.
Determine o valor de x na equação log(x-9)+2.log
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
2x-1=2
a)S=7/2 b)S=-7/2 c)S= 1/2 d)S= 13 e)S= 2
Pensei em passar o 2 que esta multiplicando com log
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
2x-1 para o expoente seguindo uma propriedade dos logaritmos e depois cortar com a raiz mas não consegui chegar a um resultado se alguem puder me ajudar eu agradeceria
-
crfsatisfaction
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jun 09, 2011 00:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em letras portugues/ingles
- Andamento: cursando
 por FilipeCaceres » Seg Jul 25, 2011 00:34
por FilipeCaceres » Seg Jul 25, 2011 00:34
Olá crfsatisfaction,
Acredito que no lugar de S seja x,não?
Veja que a condição de existência é
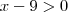
, logo

Com isso só nos resta uma alternativa que é a letra (d)
Agora vamos calcular.
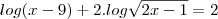
![log[(x-9)(2x-1)]=2 log[(x-9)(2x-1)]=2](/latexrender/pictures/c2f932bab486772806068e1401a7a12d.png)
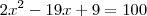
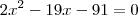

, não convém por causa da condição e existência


, confirmando o que já foi dito.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5042 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6670 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- logaritmos
por celisecorrea » Ter Set 30, 2008 17:17
- 2 Respostas
- 3362 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- LOGARITMOS
por DESESPERADA » Qua Dez 30, 2009 13:25
- 2 Respostas
- 3132 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:37
Matemática Financeira
-
- Logaritmos
por cristina » Qua Jun 02, 2010 10:07
- 1 Respostas
- 2422 Exibições
- Última mensagem por Cleyson007

Qua Jun 02, 2010 13:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 2x-1=2
2x-1=2![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 2x-1 para o expoente seguindo uma propriedade dos logaritmos e depois cortar com a raiz mas não consegui chegar a um resultado se alguem puder me ajudar eu agradeceria
2x-1 para o expoente seguindo uma propriedade dos logaritmos e depois cortar com a raiz mas não consegui chegar a um resultado se alguem puder me ajudar eu agradeceria

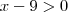 , logo
, logo 
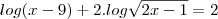
![log[(x-9)(2x-1)]=2 log[(x-9)(2x-1)]=2](/latexrender/pictures/c2f932bab486772806068e1401a7a12d.png)
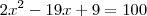
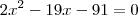
 , não convém por causa da condição e existência
, não convém por causa da condição e existência 
 , confirmando o que já foi dito.
, confirmando o que já foi dito.