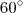por Maykids » Sex Jul 08, 2011 18:32
por Maykids » Sex Jul 08, 2011 18:32
Pessoal to tentando fazer as questões aqui mais nao consigo de jeito nenhum, porque.
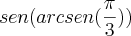
pra min o resultado disse vai ser Sen(60º)
so que eu recebi errado por ela , porque eu so expliquei que o arcsen é a inversa de seno, logo
arcsen de pi/3 sera o angulo de 60º
o que esta errado e como que eu resolvo essa questão?
desde ja agredeço
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por nietzsche » Sex Jul 08, 2011 19:15
por nietzsche » Sex Jul 08, 2011 19:15
acho que seu erro está em afirmar que:
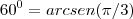
lembre-se que o ângulo

radianos, é o mesmo que 60 graus.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Maykids » Sex Jul 08, 2011 20:05
por Maykids » Sex Jul 08, 2011 20:05
ok, mais veja se eu estou certo aqui:
arcsen = seno
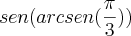
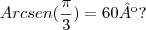
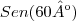
eu acho que é assim que faz. =/
mais deve ta errado msm, nao deve ser tão simples assim, e ainda mais que eu errei elas na prova.
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por Maykids » Sex Jul 08, 2011 20:10
por Maykids » Sex Jul 08, 2011 20:10
esse A ai entrou sozinho no editor, desconcidere.
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Sex Jul 08, 2011 22:23
por LuizAquino » Sex Jul 08, 2011 22:23
Como você já sabe, a função arcoseno e a função seno são inversas.
Desse modo, se

, então

.
Por exemplo:
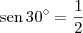

Além disso, lembre-se que se f e g são funções inversas, então f(g(x)) = x, para todo x no domínio de g.
Portanto,

, para todo x no domínio do arcoseno.
Por exemplo:

Vale destacar que esse exercício está mal posto, haja vista que o domínio da função arcoseno é um número real no intervalo [-1, 1], mas há a expressão

e temos que

(note como nesse caso devemos enxergar

como um número e não como um ângulo).
ObservaçãoMaykids escreveu:(...)

(...)
esse A ai entrou sozinho no editor, desconcidere.
Isso ocorreu porque dentro do ambiente LaTeX você usou o símbolo de grau (°) obtido do teclado. O correto é usar o comando:
- Código: Selecionar todos
[tex]60^\circ[/tex]
Resultado do comando:
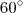
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Maykids » Sáb Jul 09, 2011 01:07
por Maykids » Sáb Jul 09, 2011 01:07
1-Quanto o º do teclado saquei vlw,
2- entao se eu não me engano a resposta dele era nao existe mesmo...mais amanha eu vo pegar a avaliação e vejo como era corretamente o exercicio.
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2264 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7482 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4960 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2972 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1998 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
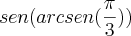

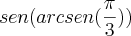

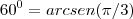
 radianos, é o mesmo que 60 graus.
radianos, é o mesmo que 60 graus.
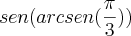
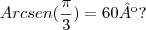
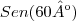


 , então
, então  .
.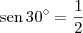

 , para todo x no domínio do arcoseno.
, para todo x no domínio do arcoseno.
 e temos que
e temos que  (note como nesse caso devemos enxergar
(note como nesse caso devemos enxergar  como um número e não como um ângulo).
como um número e não como um ângulo).