 por igorcamilo » Seg Jun 27, 2011 21:08
por igorcamilo » Seg Jun 27, 2011 21:08
Os ponteiros das horas, dos minutos e dos segundos de um relógio indicam zero hora. Até às horas do mesmo dia, os ponteiros dos minutos e dos segundos terão se encontrado um número de vezes igual a:
a)524
b)531
c)540
d)573
e)590
-
igorcamilo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 04, 2011 19:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matemática
- Andamento: cursando
 por Molina » Ter Jun 28, 2011 21:28
por Molina » Ter Jun 28, 2011 21:28
Boa noite, Igor.
To me achando um tremendo idiota na frente de um relógio vendo os ponteiros andarei. Isso tudo porque da forma que eu pensei o resultado obtido não consta nas alternativas, veja:
A cada minuto o ponteiro dos segundos passa
uma vez em todos os pontos do relógio, ou seja, a cada minuto ele vai passar
uma única vez pelo ponto em que o ponteiro do minuto estiver. Isso nos leva a crer que a cada 60 minutos (1 hora) o ponteiro dos segundos passou
60 vezes pelo ponteiro dos minutos. E isso nos leva a crer mais ainda que até ao meio-dia (12 horas depois) os ponteiros terão se encontrado
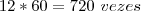
.
Alguma outra forma de pensar?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por FilipeCaceres » Ter Jun 28, 2011 23:30
por FilipeCaceres » Ter Jun 28, 2011 23:30
Olá Molina,
Você não encontrou o resultado pois está faltando dados no enunciado

, observe que não foi dito que intervalo de tempo era até o meio-dia.
Olá igorcamilo,
Até às ??horas do mesmo dia
Você poderia conferir o seu enunciado.
Abraço à todos.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Molina » Ter Jun 28, 2011 23:34
por Molina » Ter Jun 28, 2011 23:34
Boa noite.
FilipeCaceres escreveu:Olá Molina,
Você não encontrou o resultado pois está faltando dados no enunciado

, observe que não foi dito que intervalo de tempo era até o meio-dia.
Olá igorcamilo,
Até às ??horas do mesmo dia
Você poderia conferir o seu enunciado.
Abraço à todos.
Preciso voltar ao oftalmologista, pois li MEIO DIA ao invés de MESMO DIA.

Valeu pelo toque, Filipe.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relógio
por DanielFerreira » Qui Jul 30, 2009 17:46
- 1 Respostas
- 2662 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:09
Trigonometria
-
- Relógio
por DanielFerreira » Qui Jul 30, 2009 17:50
- 2 Respostas
- 4083 Exibições
- Última mensagem por Elcioschin

Sáb Ago 01, 2009 13:02
Desafios Médios
-
- Desafio do relógio
por ericomoura » Ter Nov 17, 2009 12:03
- 9 Respostas
- 8337 Exibições
- Última mensagem por Dan

Qui Fev 10, 2011 12:21
Desafios Difíceis
-
- Ângulo Relógio
por estudandoMat » Sex Abr 02, 2010 12:38
- 2 Respostas
- 6988 Exibições
- Última mensagem por estudandoMat

Sex Abr 02, 2010 14:49
Trigonometria
-
- Ponteiro de relógio
por Rafael16 » Seg Mai 27, 2013 22:07
- 1 Respostas
- 2520 Exibições
- Última mensagem por Molina

Ter Mai 28, 2013 19:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



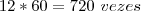 .
.

 , observe que não foi dito que intervalo de tempo era até o meio-dia.
, observe que não foi dito que intervalo de tempo era até o meio-dia.
, observe que não foi dito que intervalo de tempo era até o meio-dia.




 , avisa que eu resolvo.
, avisa que eu resolvo.

