 por hevhoram » Qui Jun 23, 2011 12:42
por hevhoram » Qui Jun 23, 2011 12:42
Um tanque tem duas torneiras. A primeira enche o tanque em 15 horas, e a segunda, em 18 horas. Estando o tanque vazio e, abrindo-se as duas torneiras durante 5 horas, enche-se uma parte do tanque. Podemos afirmar que a segunda torneira encherá o restante do tanque em:
R. 7 horas
eu ja vi problemas com uma torneira enchendo e outra esvaziando

e com duas torneiras enchendo simultaneamente
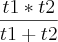
mas este tipo de questão nao sei nem como começar .. alguem pode me da uma ajuda?
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por FilipeCaceres » Qui Jun 23, 2011 15:25
por FilipeCaceres » Qui Jun 23, 2011 15:25
Façamos o seguinte,
1h
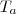
enche
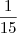
tanque
1h
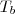
enche
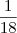
tanque
1h

enche
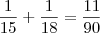
tanque
5h

enche
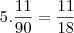
tanque
Logo nos resta encher
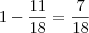
Por regra de 3 encontramos,



Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por hevhoram » Seg Jun 27, 2011 15:33
por hevhoram » Seg Jun 27, 2011 15:33
valeo obrigado
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Torneiras A e B
por Cleyson007 » Seg Jun 08, 2009 14:46
- 6 Respostas
- 7199 Exibições
- Última mensagem por ginrj

Ter Jun 09, 2009 16:52
Álgebra Elementar
-
- [Regra de Três] Exercício envolvendo torneiras
por matheus_frs1 » Ter Mai 06, 2014 10:26
- 3 Respostas
- 2964 Exibições
- Última mensagem por Russman

Sáb Mai 10, 2014 14:26
Aritmética
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12992 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10973 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15115 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

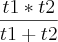


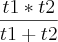

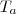 enche
enche 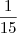 tanque
tanque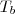 enche
enche 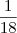 tanque
tanque enche
enche 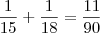 tanque
tanque enche
enche 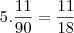 tanque
tanque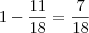






 .
.
 :
: