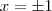Função Exponencial - Tenso!

por **jamiel** » Sáb Jun 18, 2011 03:12

Resolva a equação:

${71}^{{2x}^{3}+{4x}^{2}} = 1 {71}^{{2x}^{3}}*{71}^{{4x}^{2} = 1 {2x}^{3} + {4x}^{2} -1 = 0 -1 \left| 2 + 4 \right| -1 1 \left| 2 + 2 \right| -3 -2 \left| 2 + 4 \right| +1 -- \left| 2 + 0 \right| \left(\frac{{2x}^{3} + {4x}^{2} -1}{{-2x}^{3}-{4x}^{2}} \right):\left(\frac{x + 2 }{{2x}^{2}} \right) \left(x + 2 \right)*{2x}^{2} {2x}^{3} + {4x}^{2}$

Depois de tudo, eu chego a conclusão de q os valores de "x" são 0, 0 e -2. No entanto, surgiu uma dúvida: Como fica a situação desse "-1" em todo o processo? Eu comecei com um método de redução de uma função de terceiro para segundo grau, com o "-1" incluso, e, em seguida, parti para a divisão de polinômios. Porém, surgi, outra vez, a dúvida em relação ao "-1", mais uma vez ele permanece como um espectador. Alguém tem uma dica?

por **LuizAquino** » Dom Jun 19, 2011 12:21

Os passos de sua resolução estão errados. Acompanhe abaixo a maneira adequada.

${71}^{2x^3+4x^2} = 1$

${71}^{2x^3+4x^2} = {71}^0$

2x^3 + 4x^2 = 0

Desse modo, as soluções são x = 0 e x = -2.

por **jamiel** » Dom Jun 19, 2011 16:31

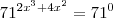
Por isso q o "1" ficava sobrando nos meus calculos. Quer dizer q eu poderia transformar o 1 em 71^0 institivamente? Não entendi muito essa parte. E neste caso, $3*{5}^{{x}^{2}} - 5*{3}^{{x}^{2}} = 0$ , o q vc faria?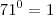

vlw ...

por **LuizAquino** » Dom Jun 19, 2011 17:01

No lado esquerdo da equação nitidamente você tem a base 71 para a potência.

Queremos que no lado direito também apareça uma potência com base 71.

Sendo assim, você deve se fazer a pergunta: 71 elevado a que número tem como resultado o valor 1?

Ora, esse número é 0, pois sabemos que ${71}^0 = 1$ .

No cado da equação $3\cdot {5}^{{x}^{2}} - 5\cdot {3}^{{x}^{2}} = 0$ , você precisa aplicar o conhecimento de logaritmos.

$3\cdot {5}^{{x}^{2}} - 5\cdot {3}^{{x}^{2}} = 0$

$3\cdot {5}^{{x}^{2}} = 5\cdot {3}^{{x}^{2}}$

$\log\left(3\cdot {5}^{{x}^{2}}\right) = \log\left(5\cdot {3}^{{x}^{2}}\right)$

$\log 3 + x^2\log 5 = \log 5 + x^2\log 3$

$x^2(\log 5 - \log 3)= \log 5 - \log 3$

x^2 = 1