 por tiagofe » Sex Mai 06, 2011 17:31
por tiagofe » Sex Mai 06, 2011 17:31
boa tarde, o resultado não bate certo com a resposta do livro.
diz que a altura h é 318.
a mim deu 183,59.
se algum puder me ajudar agradecia.
http://tinypic.com/view.php?pic=18f5n9&s=7
-
tiagofe
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Mar 31, 2011 19:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por tiagofe » Sáb Mai 07, 2011 09:22
por tiagofe » Sáb Mai 07, 2011 09:22
Boas, então a lei dos cenos e cossenos não servem para a triangulos isoceles?
Obrigado.
-
tiagofe
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Mar 31, 2011 19:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Sáb Mai 07, 2011 14:27
por MarceloFantini » Sáb Mai 07, 2011 14:27
Servem, você deve ter montado errado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por claudinho » Dom Jun 12, 2011 12:20
por claudinho » Dom Jun 12, 2011 12:20
tiagofe escreveu:Boas, então a lei dos cenos e cossenos não servem para a triangulos isoceles?
Obrigado.
Tiago, vc ta fazendo duas confusões...
1
não confunda "
lei dos senos" e "
seno"
igualmente não confunda "
lei dos cossenos" e "
cosseno"
seno, cosseno ou tangente podem ser aplicados unicamente em triangulos retangulos,
Na
lei dos senos e
lei dos cossenos,
o triângulo não precisa ser retângulo
resumo de quando aplicar "um raciocinio ou outro":para triangulos retângulos:
seno",
cosseno ou
tangentepara triangulos não-retângulos:
lei dos senos ou
lei dos cossenos2
Por vc não ter reparado no detalhe dessas diferenças,
vc aplicou
seno e
cosseno num triângulo não-retângulo ABD
e está denominado esta fórmulas aplicadas de
lei dos senosNesta questão em si era para tentar somente o raciocínio de
ou seno, (mais precisamente esta, neste exercicio)
ou cosseno
ou tgmas que só se aplicaria ao "outro" triangulo (retângulo) BCD
Conforme o Felipe fez,,
depois que provou o valor de todos os "angulos e lados" escondidos na figura
Abraços
-
claudinho
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jun 10, 2011 13:55
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Tentei, mas nao bate o resultado.
por Liliani » Qua Abr 07, 2010 17:05
- 1 Respostas
- 4181 Exibições
- Última mensagem por estudandoMat

Qua Abr 07, 2010 17:37
Desafios Fáceis
-
- [Função Composta] Resultado não bate com o do gabarito
por Richard Oliveira » Sáb Nov 12, 2011 14:59
- 3 Respostas
- 4234 Exibições
- Última mensagem por Richard Oliveira

Seg Nov 14, 2011 00:50
Funções
-
- juros simples. certo ou errado.
por Victor Gabriel » Ter Abr 16, 2013 15:34
- 3 Respostas
- 2727 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 16:40
Matemática Financeira
-
- Trigonometria exercícios simples
por Anaqino » Sex Mar 23, 2012 02:38
- 4 Respostas
- 4541 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:25
Trigonometria
-
- * Trigonometria : Questões simples que não consigo fazer!!!
por Thiago Valenca » Seg Abr 16, 2012 17:38
- 4 Respostas
- 2990 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 17:47
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






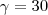
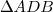 é isósceles, então
é isósceles, então 
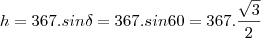
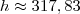
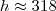







 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.