 por Claudin » Qua Jun 01, 2011 20:03
por Claudin » Qua Jun 01, 2011 20:03
Gostaria de saber o seguinte:
Quando temos
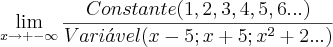
temos como resultado 0.
Porém, quando o limite tende a algum numeral seja ele 0,1,2,3,4... infinitos numeros, o resultado também seria 0
se tivesse uma constante no numerador e variáveis no denominador?
abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por carlosalesouza » Qua Jun 01, 2011 22:46
por carlosalesouza » Qua Jun 01, 2011 22:46
Dá uma olhadinha nesse arquivo... rs
http://malvadamatematica.yolasite.com/r ... IMITES.pdfbem resumido, um quebra-galho...
Mas, independente dele...
qualquer constante dividida por infinito é zero...
e infinito dividido por qualquer constante é infinito... simples assim... hehehhe
Um abraço...
Observação... a gente tá se desencontrando, né? hehhehe
sempre vejo suas chamadas na sala depois que vc já foi... tentei de mandar uma mensagem privada, mas não consegui... não costumo usar msn, mas vou te add, daí a gente pode trocar idéia... hehehe
Outro abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Claudin » Qui Jun 02, 2011 10:33
por Claudin » Qui Jun 02, 2011 10:33
Adiciona la depois Carlos.
Entao esse resuminho que você passou aqui no tópico
só fala de multiplicação entre limites com resultados infinitos e tal.
Gostaria de saber mesmo os casos especificos que eu citei!
mas valeu
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por carlosalesouza » Qui Jun 02, 2011 11:57
por carlosalesouza » Qui Jun 02, 2011 11:57
Então,
Apesar das constantes no seu exemplo se extenderem ao infinito, sempre que for uma constante, será um valor fixo, portanto finito... não importa quão grande seja, sempre haverá infinitos números maiores que ela... não é verdade?
E sempre que ela for dividida pela função de uma variável, que tende ao infinito, positivo ou negativo, f(x) será sempre infinitamente maior ou menor que a constante e o resultado da divisão será infinito positivo ou negativo, de acordo com o valor do qual x esteja se aproximando... rs
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Claudin » Qui Jun 02, 2011 16:16
por Claudin » Qui Jun 02, 2011 16:16
Certo!

Valeu Carlos
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 16:35
por LuizAquino » Qui Jun 02, 2011 16:35
carlosalesouza escreveu:Apesar das constantes no seu exemplo se estenderem ao infinito, sempre que for uma constante, será um valor fixo, portanto finito... não importa quão grande seja, sempre haverá infinitos números maiores que ela... não é verdade?
E sempre que ela for dividida pela função de uma variável, que tende ao infinito, positivo ou negativo, f(x) será sempre infinitamente maior ou menor que a constante e o resultado da divisão será infinito positivo ou negativo, de acordo com o valor do qual x esteja se aproximando... rs
Lembre-se que se
c é uma constante e
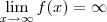
, então
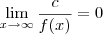
.
Vale lembrar que

sem um sinal nesse caso está representado que não importa se você está trabalhando com mais ou menos infinito.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jun 02, 2011 16:38
por Claudin » Qui Jun 02, 2011 16:38
Obrigado Luiz
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6484 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4568 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 4863 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7044 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4277 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
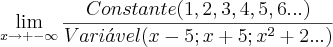

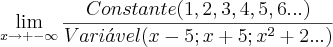






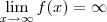 , então
, então 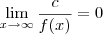 .
. sem um sinal nesse caso está representado que não importa se você está trabalhando com mais ou menos infinito.
sem um sinal nesse caso está representado que não importa se você está trabalhando com mais ou menos infinito.






