 por jaimebottas » Dom Mai 29, 2011 13:44
por jaimebottas » Dom Mai 29, 2011 13:44
Dois técnicos bancários observaram que durante o expediente de certo dia, os números de clientes que haviam atendido eram inversamente proporcionais ás suas respectivas idades: 36 e 48 anos. Se um deles atendeu 4 clientes a mais que o outro, então o total de pessoas atendidas pelo maiis velho foi:
a) 20
b) 18
c) 16
d) 14
e) 12
Eu sei que a resposta é a letra E. Mas confesso que não consigo me lembrar qual é o método a ser utilizado para se chegar a esse resultado. Me ajudem. Um abraço
-
jaimebottas
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 29, 2011 13:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Dom Mai 29, 2011 21:45
por FilipeCaceres » Dom Mai 29, 2011 21:45
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por jaimebottas » Qua Jun 01, 2011 09:21
por jaimebottas » Qua Jun 01, 2011 09:21
muito obrigado pelo esclarecimento, felipe. Deus o abençoe
-
jaimebottas
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 29, 2011 13:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11060 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10770 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12560 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3165 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5740 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


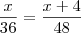
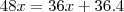






 , avisa que eu resolvo.
, avisa que eu resolvo.

