Oi Mi !
Se você "ajeitar" a equação, terá :
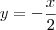
Agora, lembre-se que dizer que um ponto é (a, 1) é o mesmo que dizer que o ponto tem coordenada x = a e y = 1.
Essa observação nos permitirá obter o valor de
a e de
b.
Vou calcular o de
a, você tenta calcular o de b, tá certo :
de :
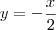
temos que y = 1 e x = a. Portanto :

ou melhor :

O que nos leva a :
a = -2Logo, um dos pontos, aquele que você disse que era (a, 1), é na verdade (-2, 1)
Ache agora o ponto (2,b) e , em seguida, a distância entre os dois pontos.
Se você ainda estiver em dúvida, post seus resultados.
Um abraço.
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) .
.![\sqrt[]{(Xb-Xa)² + (Yb-Ya)²} \sqrt[]{(Xb-Xa)² + (Yb-Ya)²}](/latexrender/pictures/b23b4db3b684f2b0859bc34203699ec1.png)
![\sqrt[]{4-4a+a²-b+1} \sqrt[]{4-4a+a²-b+1}](/latexrender/pictures/53a84f7df5ff2e2339e7fa3cad841e15.png) .
.
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) .
.![\sqrt[]{(Xb-Xa)² + (Yb-Ya)²} \sqrt[]{(Xb-Xa)² + (Yb-Ya)²}](/latexrender/pictures/b23b4db3b684f2b0859bc34203699ec1.png)
![\sqrt[]{4-4a+a²-b+1} \sqrt[]{4-4a+a²-b+1}](/latexrender/pictures/53a84f7df5ff2e2339e7fa3cad841e15.png) .
.
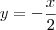
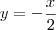




 .
.
 :
: