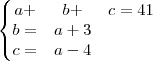por guilhermearisio » Dom Mai 22, 2011 16:12
por guilhermearisio » Dom Mai 22, 2011 16:12
1. Um nutricionista está preparando uma refeição com 2 alimentos A e B. Cadas grama do alimenta A contém 2 unidades de próteina, 3 unidades de carbroidato e 2 unidades de gordura. Cada grama do alimento B contém 4 unidades de Carbroidato 4 unidades de próteina e 3 unidades de gordura,. Essa refeição devera fornecer exatamente 400 unidades de proteinas e 500 unidades de carbroidatos.
A quantidade de gordura que esta refeição ira fornecer e?
2. André, Bento e Carlos têm, juntos, 41 anos. Sabe-se que Bento e 3 anos mias velho que André e Carlos 4 anos mias jovem que André. Se as idade de, André Bento e Carlos são respectivamente, a, b e c, então o valor de 2a-b-c é?
Meu problema e que eu não sei montar as equações, então se vcs puderem monta-las pra mim e explicar como fizeram eu agradeço.
-
guilhermearisio
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 22, 2011 16:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1° ano
- Andamento: cursando
 por DanielRJ » Dom Mai 22, 2011 20:08
por DanielRJ » Dom Mai 22, 2011 20:08
guilhermearisio escreveu:2. André, Bento e Carlos têm, juntos, 41 anos. Sabe-se que Bento e 3 anos mias velho que André e Carlos 4 anos mias jovem que André. Se as idade de, André Bento e Carlos são respectivamente, a, b e c, então o valor de 2a-b-c é?
Primeira equação:
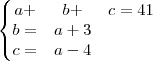
Arrumando:

agora só escalonar e chegar nestes valores.
a=14
c=10
b=17
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por guilhermearisio » Dom Mai 22, 2011 23:19
por guilhermearisio » Dom Mai 22, 2011 23:19
Sem querer abusar da sua boa vontade mias ja abusando, eu nai sei fazer ( o Professor ainda não passou ) este negocio de escalonar, olhei pra todo lado na net e continuou não dando conta se vc poder fazer pra mim.
-
guilhermearisio
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 22, 2011 16:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1° ano
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dois Problemas De P.A
por Guedes » Sex Out 08, 2010 13:44
- 5 Respostas
- 4539 Exibições
- Última mensagem por Augusto Evaristo

Sex Out 15, 2010 23:40
Progressões
-
- Resolução de Problemas de Matemática
por davssilva » Qua Mar 03, 2010 14:06
- 3 Respostas
- 9099 Exibições
- Última mensagem por davssilva

Qua Mar 03, 2010 18:37
Dúvidas Pendentes (aguardando novos colaboradores)
-
- ajuda urgente resolução de problemas
por MiguelSantos » Sáb Fev 23, 2008 08:36
- 2 Respostas
- 10965 Exibições
- Última mensagem por MiguelSantos

Dom Fev 24, 2008 07:23
Álgebra Elementar
-
- Problemas de 1 grau
por henriquefreitas » Dom Abr 24, 2011 06:27
- 1 Respostas
- 2041 Exibições
- Última mensagem por SidneySantos

Dom Abr 24, 2011 08:03
Álgebra Elementar
-
- Problemas de 1 grau
por henriquefreitas » Dom Abr 24, 2011 17:30
- 6 Respostas
- 3509 Exibições
- Última mensagem por LuizAquino

Dom Abr 24, 2011 21:25
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.