 por joaofonseca » Seg Mai 16, 2011 19:50
por joaofonseca » Seg Mai 16, 2011 19:50
Pela definição de sequência (sucessão) sei que o dominio é
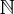
. No entanto surgiu-me uma dúvida.
Será o conjunto dos inteiros não nulos {1,2,3,4,5,6,7....} ou dos inteiros não negativos
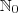
, {0,1,2,3,4,5,6,7....}.
Nos livros que utilizo o 0 não entra nos
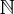
, mas na internet encontrei uma abordagem as sequências com base nos
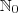
.Pode parecer um promenor, mas não é!
Imaginemos a sucessão
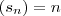
. Se o dominio for
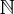
temos que o primeiro termo é 1, se o dominio for
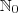
, o primeiro termo é 0.
Existe alguma convenção?
Normalmente qual o conjunto que utilizam para o estudo das sequências?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Ter Mai 17, 2011 01:38
por Molina » Ter Mai 17, 2011 01:38
Boa noite, Joao Fonseca.
Quando estudei sequências, lembro-me muito bem que o professor definia primeiramente excluindo o 0, daí chegava em algum teorema que o 0 precisava fazer parte do domínio, daí tínhamos que mudar todas as notações anteriores e assim foi por várias vezes. Acredito que isso aconteceu porque ele não estava seguinte uma única referência bibliográfica e os autores usavam diferentes domínios, dependendo de onde eles queriam chegar. Por fim, acho que se ele tivesse seguido apenas uma dos dois modos chegaria nos mesmos resultados.
Esta dúvida é semelhante a autores incluirem (ou não) o 0 nos naturais...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Ter Mai 17, 2011 02:11
por MarceloFantini » Ter Mai 17, 2011 02:11
Também estudo sequências com os naturais sem o zero. Já ouvi dizer que é por razões técnicas que facilitam outros detalhes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Ter Mai 17, 2011 02:21
por FilipeCaceres » Ter Mai 17, 2011 02:21
Eu também uso sem o zero a não ser que venho especificado que é os naturais não negaticos
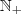
.
Abraço à todos.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por MarceloFantini » Ter Mai 17, 2011 02:25
por MarceloFantini » Ter Mai 17, 2011 02:25
Inteiros não negativos, naturais, mesmo com o zero, sempre são não-negativos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Ter Mai 17, 2011 02:52
por FilipeCaceres » Ter Mai 17, 2011 02:52
Editado
percebi um erroooo
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Ter Mai 17, 2011 02:57
por FilipeCaceres » Ter Mai 17, 2011 02:57
Marcelo você esta correto cometi uma gafe

Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Ter Mai 17, 2011 12:25
por LuizAquino » Ter Mai 17, 2011 12:25
No contexto do ensino fundamental ou médio, a convenção é que 0 é um elemento do conjunto dos naturais.
Tanto é assim que usamos a notação

para representar o conjunto dos naturais sem o zero.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3802 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3135 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2771 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Dominio] Cálculo 2- Domínio
por Saturnino Nataniel » Seg Fev 25, 2013 14:09
- 2 Respostas
- 1618 Exibições
- Última mensagem por timoteo

Ter Abr 09, 2013 12:00
Cálculo: Limites, Derivadas e Integrais
-
- Sequencia
por Amparo » Dom Mar 09, 2008 16:26
- 3 Respostas
- 3470 Exibições
- Última mensagem por nietzsche

Sex Set 02, 2011 00:42
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
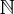 . No entanto surgiu-me uma dúvida.
. No entanto surgiu-me uma dúvida.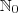 , {0,1,2,3,4,5,6,7....}.
, {0,1,2,3,4,5,6,7....}.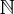 , mas na internet encontrei uma abordagem as sequências com base nos
, mas na internet encontrei uma abordagem as sequências com base nos 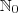 .Pode parecer um promenor, mas não é!
.Pode parecer um promenor, mas não é!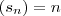 . Se o dominio for
. Se o dominio for 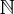 temos que o primeiro termo é 1, se o dominio for
temos que o primeiro termo é 1, se o dominio for 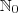 , o primeiro termo é 0.
, o primeiro termo é 0.




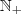 .
.
 para representar o conjunto dos naturais sem o zero.
para representar o conjunto dos naturais sem o zero.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.