em 14:32 aparece uma expressao pela qual tenho dúvida
em comparaçao com outras.
Melhor dizendo esse limite:
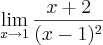
Gostaria de saber porque a resposta do limite do denominador
foi de
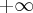 , porque em vídeos anteriores foi exposto um exemplo
, porque em vídeos anteriores foi exposto um exemplo![f(x)= \frac{\sqrt[]{x^2+9}-3}{x^2} f(x)= \frac{\sqrt[]{x^2+9}-3}{x^2}](/latexrender/pictures/1c81f941d6ca1f00e28bc80d0fa85c37.png)
foi pedido para calcular o
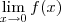
e como resposta,através das propriedades operatórias, houve uma indeterminação

Resumindo, só posso considerar uma indeterminação quando for
 ? Ou posso considerar
? Ou posso consideraro denominador sendo 0, uma indeterminação tambem? Por isso nao compreendi, o porque da resposta ser
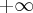
obrigado.


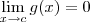 e
e 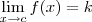 , com
, com 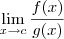 não é uma indeterminação. Nós teremos que
não é uma indeterminação. Nós teremos que 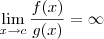 , sendo que teremos mais ou menos infinito dependendo do sinal de
, sendo que teremos mais ou menos infinito dependendo do sinal de 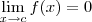 , então
, então 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.