Duvida no Teorema do valor intermediário.

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Duvida no Teorema do valor intermediário.

Regras do fórum
Responder

Duvida no Teorema do valor intermediário.

Mensagempor TheoFerraz » Sáb Abr 30, 2011 19:32

Preciso usar o teorema do valor intermediário pra resolver um exercicio aqui... To sem o meu guidorizzi e sem o meu stewart entao to vagando a internet em busca de ajuda =P, acho que essa é a minha ultima parada.

O exercicio é o seguinte:

prove que a equação 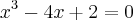{x}^{3}-4x+2=0 adimite 3 raízes reais distintas.

é provavel que exista mil maneiras de faze-lo, mas ele ta na lista que o professor passou sobre limites de sequencias e teorema do valor intermediario entao acho que deve ser resolvido usando esse maldito teorema. Em fim, qualquer ajuda é valida, Muitíssimo obrigado! até mais.
TheoFerraz
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 107
Registrado em: Qua Abr 13, 2011 19:23
Formação Escolar: GRADUAÇÃO
Área/Curso: Bacharelado em Física
Andamento: cursando
Voltar ao topo

Re: Duvida no Teorema do valor intermediário.

Mensagempor LuizAquino » Sáb Abr 30, 2011 19:39

Eu gostaria de recomendar que você assista ao vídeo:
04. Cálculo I - Limites e Continuidade
http://www.youtube.com/watch?v=NOPEwktLxgw

Nesse vídeo há um exercício usando o Teorema do Valor Intermediário. Procure mais ou menos no tempo "12:07" do vídeo.
Editado pela última vez por LuizAquino em Sáb Abr 30, 2011 19:40, em um total de 1 vez.
professoraquino.com.br | youtube.com/LCMAquino | @lcmaquino

"Sem esforço, não há ganho."
Dito popular.
Avatar do usuário
LuizAquino
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 2654
Registrado em: Sex Jan 21, 2011 09:11
Localização: Teófilo Otoni - MG
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Mestrado - Modelagem Computacional
Andamento: formado
Voltar ao topo

Re: Duvida no Teorema do valor intermediário.

Mensagempor TheoFerraz » Sáb Abr 30, 2011 19:40

Otimo, obrigado! :-D
TheoFerraz
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 107
Registrado em: Qua Abr 13, 2011 19:23
Formação Escolar: GRADUAÇÃO
Área/Curso: Bacharelado em Física
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum