 por Kelvin Brayan » Ter Abr 19, 2011 13:35
por Kelvin Brayan » Ter Abr 19, 2011 13:35
Olá amigos, a questão abaixo me pareceu estranha e não entendi bem o enunciado. Será que podem me ajudar ?
(UFG) Uma videolocadora classifica seus 1000 DVD's em lançamentos e catálogos (não lançamentos). Em um final de semana, foram locados 260 DVD's, correspondendo a quatro quintos do total de lançamentos e a um quinto do total de catálogo. Portanto, o número de DVD's de catálogo locados foi
A) 80
B) 100
C) 130
D) 160
E) 180
Vejam, eu tentei fazer da seguinte maneira:
nº de DVD's da locadora = 1000 DVD's
nº de DVD's classificados como lançamento = x
nº de DVD's classificados como catálogo = 1000-x
Percebam o seguinte trecho : "Em um final de semana, foram locados 260 DVD's, correspondendo a quatro quintos do total de lançamentos e a um quinto do total de catálogo". Então, num seria 260 = 4x/5 = 1000-x/5 ?
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por FilipeCaceres » Ter Abr 19, 2011 14:27
por FilipeCaceres » Ter Abr 19, 2011 14:27
Uma videolocadora classifica seus 1.000 DVDs em lançamento e catálogo (não lançamentos)
Assim temos,

(i)
Em um final de semana, foram locados 260 DVDs, correspondendo a quatro quintos do total de lançamentos e um quinto do total de catálogo
Logo,
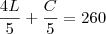
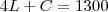
(ii)
Fazendo (ii)-(i) temos,
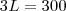

Logo,
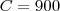
Como no final se semana foi locado um quinto do total de catálogo, temos
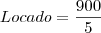
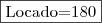
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Kelvin Brayan » Ter Abr 19, 2011 14:35
por Kelvin Brayan » Ter Abr 19, 2011 14:35
Ahhhh entendi agora, valeu ein !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Estranha
por OtavioBonassi » Sáb Jan 15, 2011 14:57
- 6 Respostas
- 3113 Exibições
- Última mensagem por Santa Lucci

Qui Fev 03, 2011 15:38
Cálculo: Limites, Derivadas e Integrais
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15118 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5034 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 (i)
(i)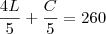
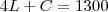 (ii)
(ii)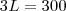

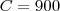
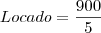
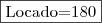
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
