Olá Fabio,
Desculpe a demora em responder, mas é que comecei a seguir uma série de sites sobre o assunto que me levaram até aqui:
http://en.wikipedia.org/wiki/Pochhammer_symbol, uma página da Wikipedia falando sobre o símbolo de Pochhammer, que representa o "rising sequential product" ou fatorial ascendente (não sei se a tradução é exatamente essa), que guarda grande similaridade com a tal expressão inicial que postei. Pesquisando mais um puco, cheguei a esse PDF:
http://www.escolademestres.com/qedtexte/tomo1serieamostra.pdf, um manual de seqüências e séries. Lá pela página 14 ele resolve o mesmo problema usando o tal produto fatorial, com a diferença que lá ele usa o descendente e naquela demonstração que postei acredito que tenha sido usado o ascendente.
É mais ou menos assim: Seja
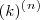
um polinômio fatorial da forma
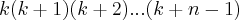
Considerando que:
Podemos exprimir um polinômio
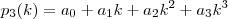
em função dos polinômios fatoriais
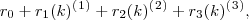
sendo
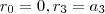
e

os restos das divisões abaixo:
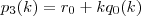

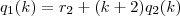
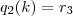
Achando esses restos
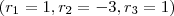
, já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:
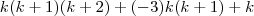
Se não quisermos obter esses restos, basta atribuir

como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de
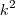
e
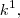
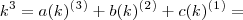
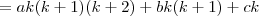
E aqui finalmente a bendita expressão aparece!
Bem, é isso. Se eu escrevi alguma besteira, por favor me corrijam...
Obrigado pela ajuda, Fabio.
Abraço.
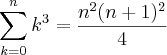 , o que é equivalente a
, o que é equivalente a 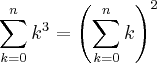
 em
em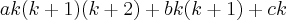
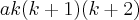 foi fatorado de
foi fatorado de 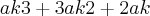 , que
, que 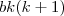 foi fatorado de
foi fatorado de 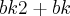 e
e 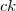 de
de 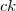


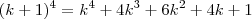
 de
de  a
a  , escrevemos assim:
, escrevemos assim: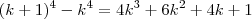
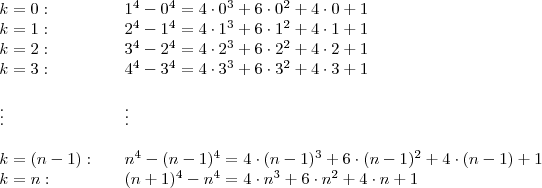



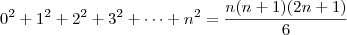

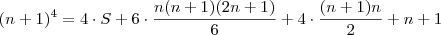
 , obtemos:
, obtemos:![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)

 fazendo a expansão de
fazendo a expansão de 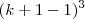 , como se fosse
, como se fosse 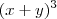 considerando
considerando 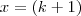 e
e 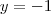 e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.
e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.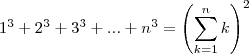

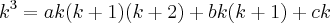
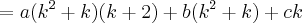
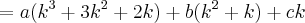
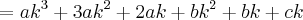
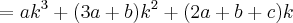

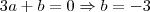



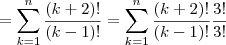
![=3!\sum_{k=1}^{n}\frac{(k+2)!}{(k-1)!3!}=3![C(3,3)+...+C(n+2,3)] =3!\sum_{k=1}^{n}\frac{(k+2)!}{(k-1)!3!}=3![C(3,3)+...+C(n+2,3)]](/latexrender/pictures/0f32f69c690f7d5eeba58eaefe11a409.png)
![=3![C(n+3,4)] =3![C(n+3,4)]](/latexrender/pictures/3bc0ff02fadcd0c7585a8e2ce37f28a7.png) (pelo teorema das colunas do triângulo de Pascal)
(pelo teorema das colunas do triângulo de Pascal)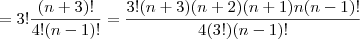
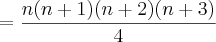
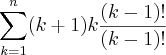
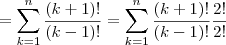
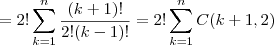
![=2![C(2,2)+C(3,2)+...+C(n+1,2)]=2![C(n+2,3)] =2![C(2,2)+C(3,2)+...+C(n+1,2)]=2![C(n+2,3)]](/latexrender/pictures/5049f994e27110d41dfe241cfc50e923.png) (pelo teorema das colunas)
(pelo teorema das colunas)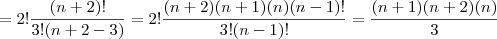
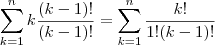
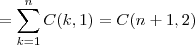 (pelo teorema das colunas)
(pelo teorema das colunas)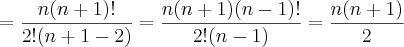
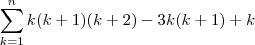
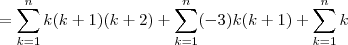
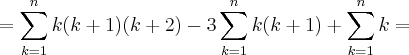
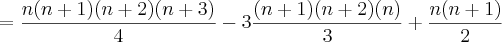

![=\frac{n(n+1)[3(n+2)(n+3)-12(n+2)+6n]}{12} =\frac{n(n+1)[3(n+2)(n+3)-12(n+2)+6n]}{12}](/latexrender/pictures/9bccca4cf5f59885edb45684aa6dc608.png)
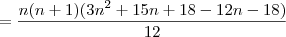
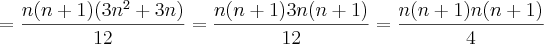
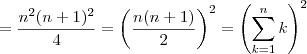
 .
.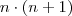 .
.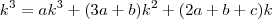
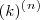 um polinômio fatorial da forma
um polinômio fatorial da forma 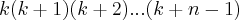
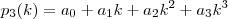 em função dos polinômios fatoriais
em função dos polinômios fatoriais 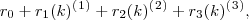 sendo
sendo 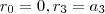 e
e  os restos das divisões abaixo:
os restos das divisões abaixo: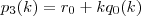

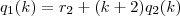
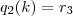
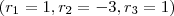 , já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:
, já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja: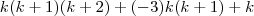
 como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de
como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de 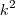 e
e 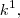
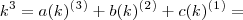
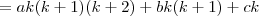

 , assentamos segmentos sucessivos de comprimentos
, assentamos segmentos sucessivos de comprimentos 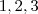 etc. e finalmente um de comprimento
etc. e finalmente um de comprimento  .
. perpendicular a
perpendicular a 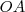 , de modo que
, de modo que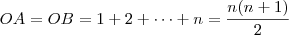
![S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I) S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I)](/latexrender/pictures/ef1e8ba07673690d2ed033da1ee52ff1.png)
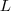 , indicadas na figura:
, indicadas na figura:
 ? Essa região pode ser dividida em dois retângulos, como na figura. Assim
? Essa região pode ser dividida em dois retângulos, como na figura. Assim![L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right] L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right]](/latexrender/pictures/dc5e67880aa252f02d42941ed68fe34a.png)
![= \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3 = \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3](/latexrender/pictures/498ab8afa9df2fb164437055465b4ad7.png)
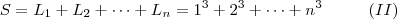
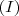 e
e 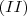 temos
temos![1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2 1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/0bd14a9561c0c92449b75c5655e22aa0.png)
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.