![f(x)=\frac{3}{5}x\sqrt[3]{x^2}+\frac{3}{2}x\sqrt[3]{x}+x](/latexrender/pictures/9ba236e43230f07d8d593ec26db39252.png "f(x)=\frac{3}{5}x\sqrt[3]{x^2}+\frac{3}{2}x\sqrt[3]{x}+x")
R.:
![f'(x)=(\sqrt[3]{x}+1)^2](/latexrender/pictures/fd9f3539665ac07853181db059988911.png "f'(x)=(\sqrt[3]{x}+1)^2")
Então, nesse exercício teríamos que primeiro utilizar a álgebra das derivadas e depois usar a "tabela de derivadas".Eu pensei em separar assim:
![f'(x)=x'\:(\frac{3}{5}\sqrt[3]{{x}^{2}})'+x'(\frac{3}{2}\sqrt[3]{x})+x'](/latexrender/pictures/57ceff89c0483737f5d2eb5ce13692b5.png "f'(x)=x'\:(\frac{3}{5}\sqrt[3]{{x}^{2}})'+x'(\frac{3}{2}\sqrt[3]{x})+x'")
Só que se eu fizesse isso eu poderia fazer isso também:
![f'(x)=\frac{3}{5}'\:(x\sqrt[3]{{x}^{2}})'...](/latexrender/pictures/93e3467338157842fd9558fe9c270a06.png "f'(x)=\frac{3}{5}'\:(x\sqrt[3]{{x}^{2}})'...")
Ai a derivada daria zero.Então deve estar errada a minha idéia.Eu teria que usar que tipo de técnica para derivar essa função?
Outras dúvida, eu queria saber se para derivar uma função usando a definição, tanto faz eu usar esse limite
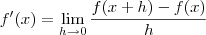ou esse 
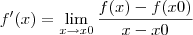, ou seja, eles são equivalentes, vão dar a mesma derivada?Sem querer abusar, poderia verificar se eu resolvi corretamente esse exercício, onde ele pede para derivar e simplificar:
http://img13.imageshack.us/i/derivada.png/
Muito obrigado.
![x \sqrt[3]{x^2} = x \cdot x^{\frac{2}{3}} = x^{\frac{5}{3}}](/latexrender/pictures/248f4455db68774e5c2344031444614c.png "x \sqrt[3]{x^2} = x \cdot x^{\frac{2}{3}} = x^{\frac{5}{3}}")
![x\sqrt[3]{x} = x \cdot x^{\frac{1}{3}} = x^{\frac{4}{3}}](/latexrender/pictures/888e939381febca0e459210039bd7712.png "x\sqrt[3]{x} = x \cdot x^{\frac{1}{3}} = x^{\frac{4}{3}}")
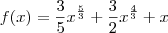
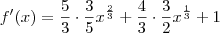
![\therefore f'(x) = x^{\frac{2}{3}} + 2 x^{\frac{1}{3}} + 1 = (x^{\frac{1}{3}} + 1)^2 = (\sqrt[3]{x} +1)^2](/latexrender/pictures/30a4d4fb0a93882e85fa18703fef53ff.png "\therefore f'(x) = x^{\frac{2}{3}} + 2 x^{\frac{1}{3}} + 1 = (x^{\frac{1}{3}} + 1)^2 = (\sqrt[3]{x} +1)^2")
por