 por Kelvin Brayan » Ter Mar 22, 2011 00:36
por Kelvin Brayan » Ter Mar 22, 2011 00:36
Olá amigos, tenho estudado muito funções ultimamente. No entanto, há certos probleminhas que não consigo resolvê-los, como esse:
(PUC Minas) Uma função do 1º grau é tal que f(-1) = 5 e f(3) = -3. Então, f(0) é igual a
a) 0
b) 2
c) 3
d) 4
e) -1
Amigos, existe algum macete pra mim determinar a fórmula da função? E como eu faço esse exercício?
Obrigado !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Molina » Ter Mar 22, 2011 10:39
por Molina » Ter Mar 22, 2011 10:39
Bom dia, Kelvin.
Você pode encontrar a equação da reta, usando a equação fundamental da reta:
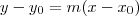
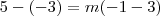


Agora que temos o coeficiente angular, vamos descobrir a equação:


Pronto! Agora é só você calcular o que a questão pede.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Kelvin Brayan » Ter Mar 22, 2011 15:17
por Kelvin Brayan » Ter Mar 22, 2011 15:17
Consegui resolver !
Muito Obrigado !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por profmatematica » Sex Mar 25, 2011 11:31
por profmatematica » Sex Mar 25, 2011 11:31
Sendo y=ax+b temos passo1¤ -a+b=5 e 3a+b=-3 temos um sistema vamos isolar o primeiro assim b= 5+a dai tu substitui no segundo termo e achara a=-2 ok? Pega -2 e substitui em b=5+a temos b=3 logo se y=ax+b temos a funcao f(x)=-2a+3, fazendo f(0)=-2.(0)+3 logo f(0)=3
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5214 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4339 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5437 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3337 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2837 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


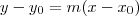
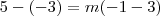








 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.