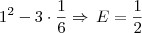por Lola » Sex Mar 18, 2011 18:39
por Lola » Sex Mar 18, 2011 18:39
(Escola Naval RJ) Sabendo que senx . cos x = 1/?6, o valor de E na expressão E=sen^6x+cos^6x é igual a?
a)1
b)-1
c)1/2
d) -1/2
e)0
Eu consegui fazer até uma parte, depois enrosquei na fatoração

:
E=(senx)^6 + (cosx)^6
E= [(senx)^2 + (cosx)^2][(senx)^4 - (senx)^2 (cosx)^2 + (cosx)^4]
E= 1 . [(senx)^4 - (senx)^2 (cosx)^2 + (cosx)^4]
E= (senx)^4 - 1/6 + (cosx)^4
Muito obrigada a quem puder me ajudar!!
-
Lola
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sex Mar 18, 2011 18:31
- Localização: São Paulo
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Sex Mar 18, 2011 19:26
por Renato_RJ » Sex Mar 18, 2011 19:26
Boa noite Lola, tudo bem ??
Eu fiz esse problema da seguinte maneira..
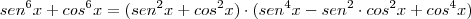
Como
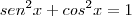
, teremos:
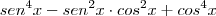
Arrumando os termos:
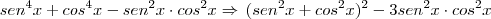
Repare que eu transformei tudo em um binômio, mas tive que incluir o termo
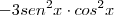
para reduzir o termo
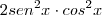
ao termo
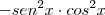
, logo teremos:
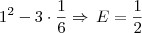
Espero que esteja certo, seria legal se você postasse o gabarito da questão..
Grato,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Lola » Sex Mar 18, 2011 21:40
por Lola » Sex Mar 18, 2011 21:40
Oi Renato!
A resposta que você obteve está correta. Muito obrigada mesmo por explicar direitinho a questão e por responder tão rápido!!
Até mais,
Lola
-
Lola
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sex Mar 18, 2011 18:31
- Localização: São Paulo
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por gustavoluiss » Sex Mar 18, 2011 23:52
por gustavoluiss » Sex Mar 18, 2011 23:52
é uma mulher e vai fazer prova pra escola naval ?
haha fake
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Renato_RJ » Sáb Mar 19, 2011 02:49
por Renato_RJ » Sáb Mar 19, 2011 02:49
gustavoluiss escreveu:é uma mulher e vai fazer prova pra escola naval ?
haha fake
Sem querer "tomar partido ou dores", mas o fato dela fazer as questões da Escola Naval não quer dizer que ela pretenda fazer a Escola Naval, talvez só queira mesmo estudar as questões típicas de uma prova bem complexa para se preparar para uma prova menos exigente, concorda ??
Por exemplo, quando eu estava na época do vestibular, eu só estudava as questões do ITA, IME, Escola Naval, USP, UNICAMP, mas nunca quis frequentar nenhuma delas, tanto que passei com excelente colocação na instituição que estou atualmente... E o fato de ser uma questão postada por uma mulher ou homem não muda o meu comportamento, se eu tiver como ajudar sempre o faço...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Mar 19, 2011 14:24
por MarceloFantini » Sáb Mar 19, 2011 14:24
Gustavo Luís, sua colocação é mal educada, preconceituosa e machista. Sugiro que você mude estes aspectos na hora que for postar no fórum.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Lola » Dom Mar 20, 2011 01:26
por Lola » Dom Mar 20, 2011 01:26
Gustavo Luís, Dúvida em um exercício da Escola Naval não significa necessariamente que eu vou fazer prova para a Escola Naval, seu boçal. Este exercício é da minha apostila de tarefa da escola, e como eu não sabia fazer eu pedi ajuda para as pessoas desse fórum. Se você não pode me ajudar com a minha dúvida, por favor, não responda ao tópico e não me encha o saco.
Seu comentário foi bem deplorável e ultrapassado, ainda mais porque foi dirigido a uma mulher cuja família é toda formada por homens e mulheres com carreira militar. A realidade do exército hoje é bem diferente da que a sua mentalidade infantil imagina. Da próxima vez, lembre-se de vir a este fórum somente para compartilhar seu conhecimento (isto é, se você tiver algum), e não a sua mediocridade.
Mais uma vez obrigada ao Renato por me ajudar com a dúvida. Ainda bem que existem pessoas como você para manter a decência e a proposta inicial deste fórum.
-
Lola
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sex Mar 18, 2011 18:31
- Localização: São Paulo
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Dan » Dom Mar 20, 2011 01:43
por Dan » Dom Mar 20, 2011 01:43
Pessoal, vamos acalmar os ânimos e evitar maiores ofensas e retaliações.
Acho que o gustavoluiss entendeu que nós não gostamos do comentário dele.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [triângulo / segmento] Ajuda em mais uma do colegio naval...
 por Joan » Sáb Jul 23, 2011 13:18
por Joan » Sáb Jul 23, 2011 13:18
- 6 Respostas
- 4696 Exibições
- Última mensagem por Joan

Seg Jul 25, 2011 16:11
Geometria Plana
-
- Questão do C.Naval
por ginrj » Ter Jul 21, 2009 15:06
- 2 Respostas
- 2079 Exibições
- Última mensagem por ginrj

Sex Jul 24, 2009 19:52
Sistemas de Equações
-
- MMC e MDC - Colégio Naval
por igorcamilo » Sáb Jun 25, 2011 21:22
- 1 Respostas
- 2042 Exibições
- Última mensagem por FilipeCaceres

Dom Jun 26, 2011 16:13
Álgebra Elementar
-
- Colégio Naval
por Joan » Seg Jul 25, 2011 16:38
- 8 Respostas
- 8355 Exibições
- Última mensagem por LuizAquino

Ter Jul 26, 2011 21:35
Álgebra Elementar
-
- Divisibilidade - Colégio naval
por igorcamilo » Sex Jun 24, 2011 19:22
- 2 Respostas
- 2475 Exibições
- Última mensagem por igorcamilo

Sex Jun 24, 2011 20:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 :
:

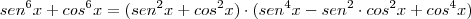
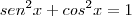 , teremos:
, teremos: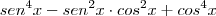
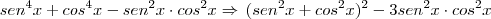
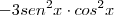 para reduzir o termo
para reduzir o termo 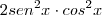 ao termo
ao termo 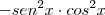 , logo teremos:
, logo teremos: