 por andersontricordiano » Sex Mar 11, 2011 13:14
por andersontricordiano » Sex Mar 11, 2011 13:14
Três números reais a,b e c satisfazem o sistema abaixo:
Além disso, eles estão em progressão geométrica , isto é, existe um número real r tal que b=ar e c=br. Determine todos os possíveis valores de r e os correspondentes valores de a , b e c.
Detalhe a resposta é:
Quando r=3,a=9,b=27 e c=81
Quando r=1/3, a=81,b=27 e c=9
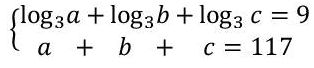
- log3a-Page-1.jpg (7.91 KiB) Exibido 1271 vezes
Por favor me ajudem a resolver esse calculo.
Grato quem me ajudar!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Mar 11, 2011 21:23
por LuizAquino » Sex Mar 11, 2011 21:23
DicaSe a, b e c formam, nessa ordem, uma p.g. de razão r, então temos a sequência
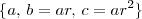
.
Lembre-se da propriedade de logaritmo:

Por fim, lembre-se da definição de logaritmo:
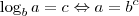
, com
,
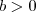
e
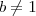
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4260 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4730 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25583 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4246 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2900 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


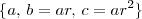 .
.
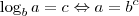 , com
, com 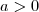 ,
, 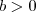 e
e 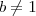 .
.
