O exercício foi da prova da (FUVEST-1999). O texto original da questão é:
(FUVEST-SP) Dados dois números reais a e b que satisfazem as desigualdades
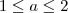
e
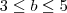
, pode-se afirmar que:
A)
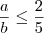
B)
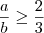
C)
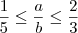
D)
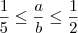
E)
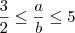
O gabarito oficial é C). Tanto a prova quanto o gabarito estão disponíveis no endereço:
FUVEST Provas 1999http://www.fuvest.br/vest1999/provas/provas.stmAgora, vamos a resolução.
Nós vamos precisar de três propriedades das inequações:
(i) Se
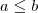
e
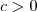
, então
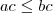
.
(ii) Se
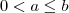
, então
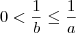
.
(iii) Se
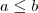
e
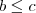
, então
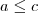
.
Multiplicando-se a inequação
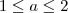
por

(que é um número positivo), obtemos
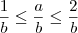
.
Da inequação
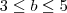
, temos que
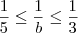
.
Portanto, de
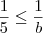
e
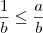
concluímos que
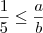
.
Multiplicando-se a inequação
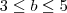
por

(que é um número positivo), obtemos
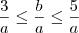
, ou ainda,
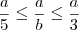
.
Multiplicando-se a inequação
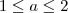
por

, temos que
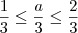
.
Portanto, de
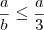
e
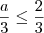
concluímos que
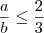
.
Desse modo, temos que
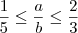
.
Observaçõesa > 1
b > 3
a/b > 1/3
Isso é falso! Note que se a=9/8 e b=9/2 nós temos que 1 < a < 2 e 3 < b < 5, mas a/b < 1/3.
a < 2
b < 5
a/b < 2/5
Isso também é falso! Note que se a=7/4 e b=7/2 nós temos que 1 < a < 2 e 3 < b < 5, mas a/b > 2/5.
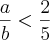
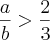
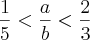
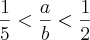
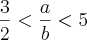

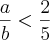
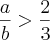
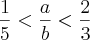
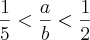
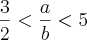



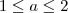 e
e 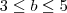 , pode-se afirmar que:
, pode-se afirmar que: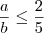
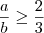
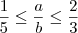
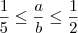
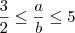
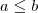 e
e 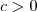 , então
, então 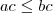 .
.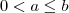 , então
, então 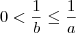 .
.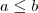 e
e 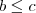 , então
, então 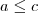 .
.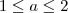 por
por  (que é um número positivo), obtemos
(que é um número positivo), obtemos 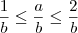 .
.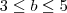 , temos que
, temos que 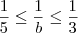 .
.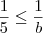 e
e 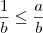 concluímos que
concluímos que 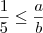 .
.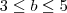 por
por  (que é um número positivo), obtemos
(que é um número positivo), obtemos 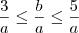 , ou ainda,
, ou ainda, 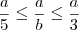 .
.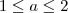 por
por  , temos que
, temos que 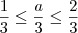 .
.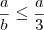 e
e 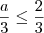 concluímos que
concluímos que 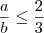 .
.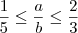 .
.

 .
.



