 por Mandu » Dom Out 24, 2010 15:41
por Mandu » Dom Out 24, 2010 15:41
Uma liga metálica de 100kg é constituída de 20% de ouro e 5% de prata. Quantos quilogramas de ouro e de prata devem ser adicionados a esta liga para se obter uma outra cuja constituição seja de 30% de ouro e 10% de prata?
-
Mandu
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Set 20, 2010 14:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Adriano Tavares » Ter Mar 08, 2011 22:02
por Adriano Tavares » Ter Mar 08, 2011 22:02
Olá, Mandu.
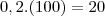
--> total de quilos de ouro
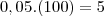
--> total de quilos de prata

--> quantidade de ouro

quantidade de prata
Como serão acrescentados ouro e prata na liga, e a nova quantidade de ouro e prata devem representar respectivamente

e

do total teremos:
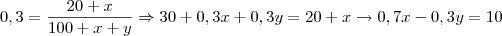

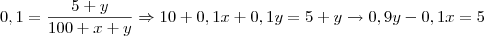

Resolvendo esse sistema encontrtaremos
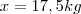
e
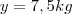
-
Adriano Tavares
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Mar 07, 2011 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em automação industrial
- Andamento: formado
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



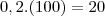 --> total de quilos de ouro
--> total de quilos de ouro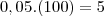 --> total de quilos de prata
--> total de quilos de prata --> quantidade de ouro
--> quantidade de ouro quantidade de prata
quantidade de prata e
e  do total teremos:
do total teremos: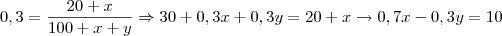

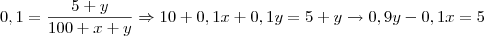

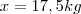 e
e 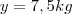



 , avisa que eu resolvo.
, avisa que eu resolvo.

