
Se aplicarmos a regra de L'Hôpital duas vezes, teremos:
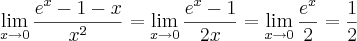

ARCS escreveu:Como calcular esse limite algebricamente sem usar as regras de L'Hôpital?
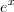 em torno de a=0:
em torno de a=0: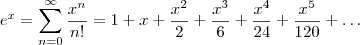
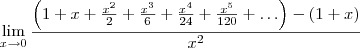
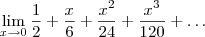
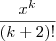 , sendo k>=1. Como x tende a zero, cada parcela dessa tenderá a zero, portanto:
, sendo k>=1. Como x tende a zero, cada parcela dessa tenderá a zero, portanto: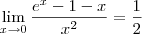


ARCS escreveu:É uma questão dos tópicos iniciais de Limites e Derivadas do livro do James Stewart.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

