jose henrique escreveu:quando vc afirma que o valor dentro raiz no primeiro membro é necessariamente positivo é levando em conta que x>3. caso fosse somente x<-3 teria solução a equação?
Sim. Faça um teste. Coloque, por exemplo, -4 (que é menor do que -3) na expressão com a raiz:
![\sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287} \sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287}](/latexrender/pictures/cb0c5a8aabbe2fde3c4772d6157cbd6e.png)
Note que o valor dentro da raiz foi positivo.
jose henrique escreveu:caso eu queira simplificar a seguinte expressão

eu poderia elevar tanto o numerador quanto o denominador ao quadrado e para eu começar a simplificar.
Não.
Se você tem apenas uma
fração e eleva o numerador e o denominador ao quadrado, então você altera a fração. Por exemplo,

é diferente
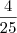
. Basta efetuar a divisão que você irá encontrar
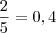
e
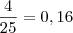
.
Por outro lado, se você tem uma
equação, então pode elevar ambos os membros da mesma ao quadrado e ela não se altera. Por exemplo,
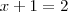
e
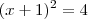
ambas tem solução

.
Para ser mais exato, na segunda equação também poderíamos encontrar x=-3, mas isso não importa, pois perceba que tanto a primeira quanto a segunda equação tem uma solução em comum que é

.
![\frac{\sqrt[]{({x}^{2}-9)({x}^{2}+25)}}{x-3} =x+5 \frac{\sqrt[]{({x}^{2}-9)({x}^{2}+25)}}{x-3} =x+5](/latexrender/pictures/e7f0929d1e8f3b55565f57a8acb4fe34.png) , para todo x
, para todo x  -3 ou x>3
-3 ou x>3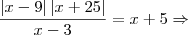 fazer isso.
fazer isso.

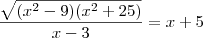 , para todo
, para todo 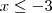 ou
ou 
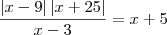 , eu posso fazer isso?
, eu posso fazer isso?
![\left(\sqrt{({x}^{2}-9)({x}^{2}+25)}\right)^2 = \left[(x-3)(x+5)\right]^2 \left(\sqrt{({x}^{2}-9)({x}^{2}+25)}\right)^2 = \left[(x-3)(x+5)\right]^2](/latexrender/pictures/2436e6c6aef4cf48931cec99d524e77e.png)
![({x}^{2}-9)({x}^{2}+25) = \left[(x-3)(x+5)\right]^2 ({x}^{2}-9)({x}^{2}+25) = \left[(x-3)(x+5)\right]^2](/latexrender/pictures/66ce122ba66a1d0dad5fafeb93e99290.png)
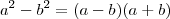 , podemos fazer:
, podemos fazer: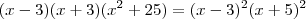
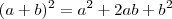 :
: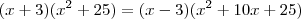

![\frac{\sqrt[]{\left({x}^{2}-9 \right)\left({x}^{2}+25 \right)}}{x-3} \frac{\sqrt[]{\left({x}^{2}-9 \right)\left({x}^{2}+25 \right)}}{x-3}](/latexrender/pictures/bdb7d29774ff3b6d9a128cb84541a3af.png)
![\sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287} \sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287}](/latexrender/pictures/cb0c5a8aabbe2fde3c4772d6157cbd6e.png)

 é diferente
é diferente 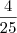 . Basta efetuar a divisão que você irá encontrar
. Basta efetuar a divisão que você irá encontrar 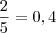 e
e 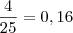 .
.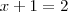 e
e 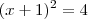 ambas tem solução
ambas tem solução  .
.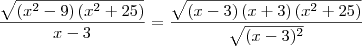
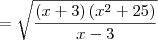 .
.
 aí podemos efetuar a simplificação já que teremos algo como
aí podemos efetuar a simplificação já que teremos algo como 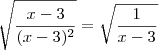 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.