 por jose henrique » Qui Fev 17, 2011 18:48
por jose henrique » Qui Fev 17, 2011 18:48
![\frac{\sqrt[]{({x}^{2}-9)({x}^{2}+25)}}{x-3} =x+5 \frac{\sqrt[]{({x}^{2}-9)({x}^{2}+25)}}{x-3} =x+5](/latexrender/pictures/e7f0929d1e8f3b55565f57a8acb4fe34.png)
, para todo x

-3 ou x>3
eu posso
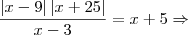
fazer isso.
na verdade eu não estou entendo esta questão do x elevado ao quadrado dentro de uma raiz, eu sei que não posso simplificar simplesmente colocando como resposta o x visto que ele está elevado ao quadrado, mas quando tem uma expressão desse jeito o que devo fazer.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por LuizAquino » Qui Fev 17, 2011 20:40
por LuizAquino » Qui Fev 17, 2011 20:40
jose henrique escreveu: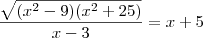
, para todo
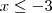
ou

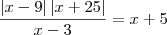
, eu posso fazer isso?
Não.
Se o objetivo for determinar o valor de x, então o correto é fazer:

Elevar ambos os membros ao quadrado:
![\left(\sqrt{({x}^{2}-9)({x}^{2}+25)}\right)^2 = \left[(x-3)(x+5)\right]^2 \left(\sqrt{({x}^{2}-9)({x}^{2}+25)}\right)^2 = \left[(x-3)(x+5)\right]^2](/latexrender/pictures/2436e6c6aef4cf48931cec99d524e77e.png)
Como a quetão diz que
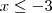
ou

, então o valor dentro da raiz que aparece no primeiro membro é necessariamante positivo. Portanto, podemos fazer a simplificação:
![({x}^{2}-9)({x}^{2}+25) = \left[(x-3)(x+5)\right]^2 ({x}^{2}-9)({x}^{2}+25) = \left[(x-3)(x+5)\right]^2](/latexrender/pictures/66ce122ba66a1d0dad5fafeb93e99290.png)
Lembrando do produto notável
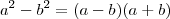
, podemos fazer:
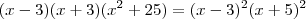
Como x é diferente de 3 (já que x>3), então podemos dividir toda a equação por (x-3). Além disso, temos o produto notável
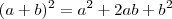
:
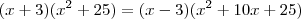
Agora, desenvolva essa equação para obter uma equação do 2º grau. A partir daí aplique a fórmula de Bháskara para achar as soluções.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jose henrique » Qui Fev 17, 2011 21:26
por jose henrique » Qui Fev 17, 2011 21:26
quando vc afirma que o valor dentro raiz no primeiro membro é necessáriamente positivo é levando em conta que x>3. caso fosse somente x<-3 teria solução a equação
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por jose henrique » Qui Fev 17, 2011 21:52
por jose henrique » Qui Fev 17, 2011 21:52
caso eu queira simplificar a seguinte expressão
![\frac{\sqrt[]{\left({x}^{2}-9 \right)\left({x}^{2}+25 \right)}}{x-3} \frac{\sqrt[]{\left({x}^{2}-9 \right)\left({x}^{2}+25 \right)}}{x-3}](/latexrender/pictures/bdb7d29774ff3b6d9a128cb84541a3af.png)
eu poderia elevar tanto o numerador quanto o denominador ao quadrado e para eu começar a simplificar.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por LuizAquino » Qui Fev 17, 2011 22:08
por LuizAquino » Qui Fev 17, 2011 22:08
jose henrique escreveu:quando vc afirma que o valor dentro raiz no primeiro membro é necessariamente positivo é levando em conta que x>3. caso fosse somente x<-3 teria solução a equação?
Sim. Faça um teste. Coloque, por exemplo, -4 (que é menor do que -3) na expressão com a raiz:
![\sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287} \sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287}](/latexrender/pictures/cb0c5a8aabbe2fde3c4772d6157cbd6e.png)
Note que o valor dentro da raiz foi positivo.
jose henrique escreveu:caso eu queira simplificar a seguinte expressão

eu poderia elevar tanto o numerador quanto o denominador ao quadrado e para eu começar a simplificar.
Não.
Se você tem apenas uma
fração e eleva o numerador e o denominador ao quadrado, então você altera a fração. Por exemplo,

é diferente
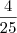
. Basta efetuar a divisão que você irá encontrar
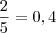
e
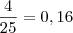
.
Por outro lado, se você tem uma
equação, então pode elevar ambos os membros da mesma ao quadrado e ela não se altera. Por exemplo,
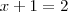
e
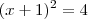
ambas tem solução

.
Para ser mais exato, na segunda equação também poderíamos encontrar x=-3, mas isso não importa, pois perceba que tanto a primeira quanto a segunda equação tem uma solução em comum que é

.
Editado pela última vez por
LuizAquino em Qui Fev 17, 2011 22:20, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jose henrique » Qui Fev 17, 2011 22:17
por jose henrique » Qui Fev 17, 2011 22:17
como eu poderia simplificar então
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por LuizAquino » Qui Fev 17, 2011 22:25
por LuizAquino » Qui Fev 17, 2011 22:25
jose henrique escreveu:como eu poderia simplificar então
Não dá para fazer muita coisa nesse caso.
Uma simplificação poderia ser:
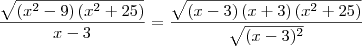
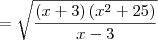
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jose henrique » Qui Fev 17, 2011 22:42
por jose henrique » Qui Fev 17, 2011 22:42
só não entendi por que vc colocou o denominador dentro de uma raiz, uma vez que ele não estava
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por LuizAquino » Qui Fev 17, 2011 22:52
por LuizAquino » Qui Fev 17, 2011 22:52
jose henrique escreveu:só não entendi por que vc colocou o denominador dentro de uma raiz, uma vez que ele não estava
Porque se temos
 não podemos
não podemos simplificar (x-3) com (x-3), pois um está dentro e ou outro está fora da raiz. Por outro lado, se fazemos

aí podemos efetuar a simplificação já que teremos algo como
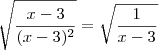
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jose henrique » Qui Fev 17, 2011 23:06
por jose henrique » Qui Fev 17, 2011 23:06
me desculpa perguntar, mas em qual regra eu posso me basear para resolver este tipo de questões, pois irei até procurar, pois com a sua resolução eu entendi o porquê da raiz do denominador, mas não compreendi como posso fazer isso sem afetar alguma regra.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por LuizAquino » Qui Fev 17, 2011 23:31
por LuizAquino » Qui Fev 17, 2011 23:31
jose henrique escreveu:me desculpa perguntar, mas em qual regra eu posso me basear para resolver este tipo de questões, pois irei até procurar, pois com a sua resolução eu entendi o porquê da raiz do denominador, mas não compreendi como posso fazer isso sem afetar alguma regra.
Para executar os passos de simplificação sem quebrar as "regras", primeiro você precisa conhecer todas as "regras", pois só assim saberá se está ou não quebrando alguma.
Para isso, você precisa começar a estudar as propriedades de potência, a estudar as propriedades de radiciação, a estudar os produtos notáveis e a estudar fatoração. Isto é, o que não falta é assunto para você estudar!

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2359 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2878 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- [SIMPLIFICAÇÃO] Simplificação expoentes
por brunnkpol » Ter Mai 07, 2013 17:00
- 1 Respostas
- 1835 Exibições
- Última mensagem por DanielFerreira

Sex Mai 10, 2013 00:40
Aritmética
-
- Simplificação!
por carmem » Ter Mai 12, 2009 23:34
- 2 Respostas
- 2007 Exibições
- Última mensagem por carmem

Qua Mai 13, 2009 11:01
Álgebra Elementar
-
- Simplificação
por Jamilly » Qua Mar 17, 2010 21:44
- 1 Respostas
- 2035 Exibições
- Última mensagem por Elcioschin

Qua Mar 17, 2010 22:04
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[]{({x}^{2}-9)({x}^{2}+25)}}{x-3} =x+5 \frac{\sqrt[]{({x}^{2}-9)({x}^{2}+25)}}{x-3} =x+5](/latexrender/pictures/e7f0929d1e8f3b55565f57a8acb4fe34.png) , para todo x
, para todo x  -3 ou x>3
-3 ou x>3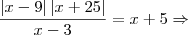 fazer isso.
fazer isso.

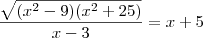 , para todo
, para todo 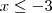 ou
ou 
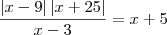 , eu posso fazer isso?
, eu posso fazer isso?
![\left(\sqrt{({x}^{2}-9)({x}^{2}+25)}\right)^2 = \left[(x-3)(x+5)\right]^2 \left(\sqrt{({x}^{2}-9)({x}^{2}+25)}\right)^2 = \left[(x-3)(x+5)\right]^2](/latexrender/pictures/2436e6c6aef4cf48931cec99d524e77e.png)
![({x}^{2}-9)({x}^{2}+25) = \left[(x-3)(x+5)\right]^2 ({x}^{2}-9)({x}^{2}+25) = \left[(x-3)(x+5)\right]^2](/latexrender/pictures/66ce122ba66a1d0dad5fafeb93e99290.png)
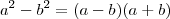 , podemos fazer:
, podemos fazer: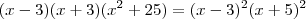
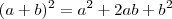 :
: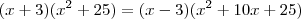

![\frac{\sqrt[]{\left({x}^{2}-9 \right)\left({x}^{2}+25 \right)}}{x-3} \frac{\sqrt[]{\left({x}^{2}-9 \right)\left({x}^{2}+25 \right)}}{x-3}](/latexrender/pictures/bdb7d29774ff3b6d9a128cb84541a3af.png)
![\sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287} \sqrt{[(-4)^2-9 ][(-4)^{2}+25]} = \sqrt{7\cdot 41} = \sqrt{287}](/latexrender/pictures/cb0c5a8aabbe2fde3c4772d6157cbd6e.png)

 é diferente
é diferente 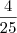 . Basta efetuar a divisão que você irá encontrar
. Basta efetuar a divisão que você irá encontrar 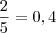 e
e 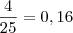 .
.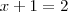 e
e 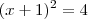 ambas tem solução
ambas tem solução  .
.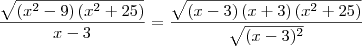
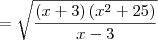 .
.
 aí podemos efetuar a simplificação já que teremos algo como
aí podemos efetuar a simplificação já que teremos algo como 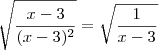 .
.