
Considerando como comprimento da secante AB a variavel "X", e o comprimento da flecha FF' a variavel "Y", qual seria a equação para determinar o raio da circunferencia?
Grato
Fred.



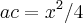
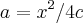
![c=\sqrt[]{(4y^2+x^2)/4} c=\sqrt[]{(4y^2+x^2)/4}](/latexrender/pictures/82fa450ec9b192c90a18c4eceef3232f.png)
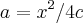
![a=x^2/4\sqrt[]{(4y^2+x^2)/4} a=x^2/4\sqrt[]{(4y^2+x^2)/4}](/latexrender/pictures/2cce5d6107658c57e65a973331d2ebe3.png)
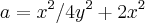
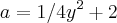
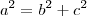
![(1/4y^2+2)^2=b^2+( \sqrt[]{(4y^2+x^2)/4} )^2 (1/4y^2+2)^2=b^2+( \sqrt[]{(4y^2+x^2)/4} )^2](/latexrender/pictures/39e8f3bc6d9a2ebb864a63dfb4b20913.png)
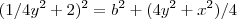
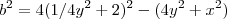
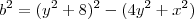
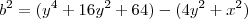
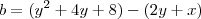 - Não sei se esta redução é coerente. é aqui que estou travando...
- Não sei se esta redução é coerente. é aqui que estou travando...
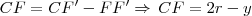
 então teremos um triângulo retângulo CAF onde:
então teremos um triângulo retângulo CAF onde: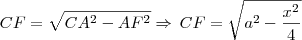
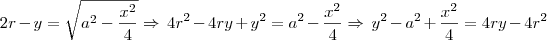

freddrago escreveu:Considerando que todo triangulo inscrito, com um dos catetos igual ao diametro é retangulo. Extendendo-se a flecha, temos uma linha que corta o centro da circunferencia que chamamos de ponto C.
Renato_RJ escreveu:(...) reparou que esse arco CAF' forma um semicírculo ? Então, podemos afirmar que o ângulo CÂF' é reto, isto é, mede 90º pois todos os ângulos que subtendem um semicírculo são retos.
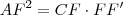
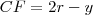 , nós obtemos que
, nós obtemos que 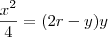 . Isolando r, nós obtemos
. Isolando r, nós obtemos 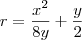 .
.
LuizAquino escreveu:
No exercício, você está considerando que AF=FB=x/2 (F é ponto médio de AB=x), FF'=y e FF' é perpendicular a AB.
Como vimos, o triângulo CAF' é retângulo. Aplicando a relação métrica que envolve a altura do triângulo retângulo e as projeções dos catetos sobre a hipotenusa, temos que
Lembrando que, nós obtemos que
. Isolando r, nós obtemos
.



Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.