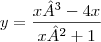
Resolvi ele até certa parte:
u =
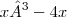 u' =
u' = 
v =
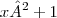 v' =
v' = 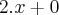
y' = u'.v-v'.u
v²
y' =
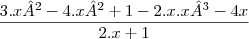
Bom ai eu me perco não sei se o processo até ai está 100% correto mais foi assim que consegui assimilar quando o professor explicou.
* Desculpem não consegui colocar o símbolo de derivado no "u e v" apresentado na formula.
** Coloquei as variáveis u e v para definirem a formula antes de derivada e depois de derivar.
*** Preciso de ajuda em como proceder pois tenho uma grande dificuldade pois não sei se devo multiplicar a primeira pela segunda parte.
Grato!


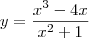

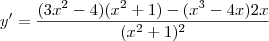
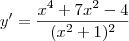


 .
.



