Olá viniciusdosreis,
Como está na resolução da questão?
Segue abaixo a minha resolução.
viniciusdosreis escreveu:b) Tem-se E=F+G se, e somente se,
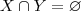
Temos que provar que:
(i)
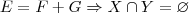
(ii)
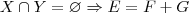 Afirmação (i)
Afirmação (i)Por hipótese, qualquer que seja a função
e em E teremos funções
f em F e
g em G tal que
e = f + g. Sendo assim, tomemos qualquer função
e em E tal que
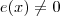
, para todo x em

. Agora, suponha que
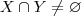
e tomemos um
k em

. Desse modo,
teríamos e(k)=f(k)+g(k)=0+0=0.
Mas, isso contraria a definição da função
e que escolhemos. Portanto, deve ocorrer
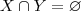
.
Afirmação (ii)Seja
e uma função qualquer em E. Podemos escrever
e como sendo:
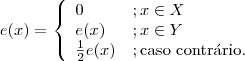
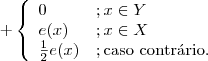
Fazendo:
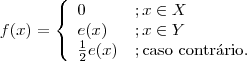
,
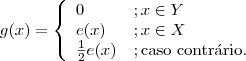
,
temos que
f está em F e
g está em G, de modo que
e=f+g. Como
e é qualquer, então temos que E=F+G.
Note que essas funções
f e
g só estão bem definidas devido a hipótese
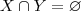
. Sem essa hipótese, tanto a função
f quanto a função
g estaria mal definida, pois para qualquer elemento em

tanto
f quanto
g daria 0 e e(x) ao mesmo tempo, o que não pode ocorrer.
viniciusdosreis escreveu:c) Tem-se
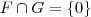
se, e somente se,
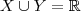
Temos que provar que:
(i)
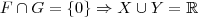
(ii)
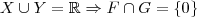 Afirmação (i)
Afirmação (i)Seja
e uma função em E definida por
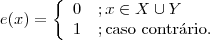
. Sendo assim,
e está em

. Mas, por hipótese em

só temos o elemento neutro do espaço de funções E (isto é, a função n(x)=0, para qualquer x em

). Portanto,
e deve também ser o elemento neutro do espaço E. Mas, para que
e seja o elemento neutro desse espaço ele deve levar todos os valores de

em 0, o que só ocorre se
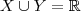
na definição de
e.
Afirmação (ii)Seja
e qualquer função em E tal que
e(x)=0 para qualquer elemento em

. Sendo assim,
e está em

. Além disso, como por hipótese
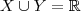
, então
e leva qualquer valor de

em 0. Portanto,
e só pode ser a função que é o elemento neutro do espaço de funções E (lembre-se que em qualquer espaço o elemento neutro é único). Logo, temos que
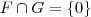
.
viniciusdosreis escreveu:d) Vale
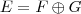
se, e somente se,
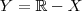
.
Temos que provar que:
(i)
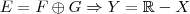
(ii)

Para resolver o quesito d), lembre-se que há um teorema que garante que se F e G são subespaços de um espaço E temos que:
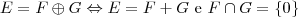 Afirmação (i)
Afirmação (i)Por hipótese,
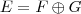
. Portanto, sabemos pelo teorema citado acima que deve ocorrer que E = F + G e
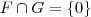
. Usando os resultados dos quesitos (b) e (c), temos que
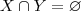
e
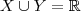
. Logo, temos que
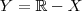
.
Afirmação (ii)Por hipótese,
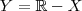
. Disso segue que
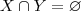
e
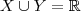
. Usando os resultados dos quesitos (b) e (c), temos que E = F + G e
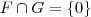
. Logo, pelo teorema citado acima, temos que
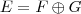
.
 IR, sejam
IR, sejam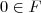 ; é claro que o conjunto F contem o elemento neutro, uma vez que para
; é claro que o conjunto F contem o elemento neutro, uma vez que para 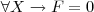
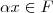 , sendo
, sendo 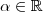 e
e 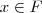


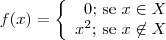 é uma delas.
é uma delas.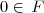 .
.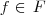 , então
, então 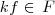 , sendo k um número real qualquer.
, sendo k um número real qualquer.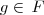 , então
, então 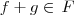 .
.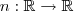 definida por n(x)=0. Note que essa função servirá como elemento neutro para a soma entre funções e além disso ela pertence a F, já que ela é zero para x em X (ora, se ela é zero para qualquer valor em
definida por n(x)=0. Note que essa função servirá como elemento neutro para a soma entre funções e além disso ela pertence a F, já que ela é zero para x em X (ora, se ela é zero para qualquer valor em  , é claro que ela será zero para um subconjunto X de
, é claro que ela será zero para um subconjunto X de 
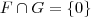 se, e somente se,
se, e somente se, 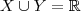 .
. e
e  . Temos X e Y subconjuntos de
. Temos X e Y subconjuntos de 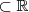 , sejam
, sejam ;
;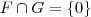 se, e somente se,
se, e somente se, 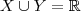 ;
;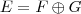 se, e somente se,
se, e somente se, 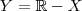 ;
;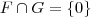 , sejam
, sejam 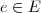 ,
, 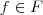 e
e 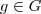 , temos que e=f+g.
, temos que e=f+g.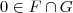 .
.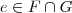 , ou seja,
, ou seja, 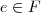 e
e 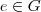 . Para que
. Para que 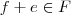 e
e 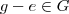 . Como temos um unico f e g satisfazendo e=f+g; entao f=f+e e g=g-e. Portanto e=0. Logo
. Como temos um unico f e g satisfazendo e=f+g; entao f=f+e e g=g-e. Portanto e=0. Logo 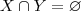
 não tivesse apenas o zero. Correto? Ou estou confundindo?
não tivesse apenas o zero. Correto? Ou estou confundindo?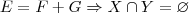
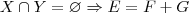
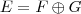 , o que não faz parte de sua hipótese. A sua hipótese é que E=F+G. Vale lembrar que soma direta (denotada por
, o que não faz parte de sua hipótese. A sua hipótese é que E=F+G. Vale lembrar que soma direta (denotada por  ) e soma (denotada por +) são duas coisas distintas.
) e soma (denotada por +) são duas coisas distintas.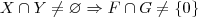
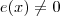 , para todo x em
, para todo x em 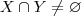 e tomemos um
e tomemos um  . Desse modo,
. Desse modo, 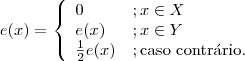
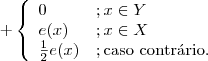
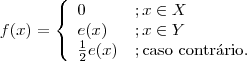 ,
,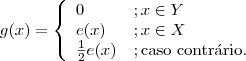 ,
,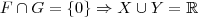
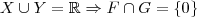
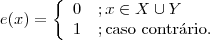 . Sendo assim,
. Sendo assim,  . Sendo assim,
. Sendo assim,  . Além disso, como por hipótese
. Além disso, como por hipótese 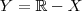 .
.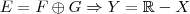

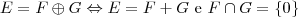
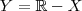 . Disso segue que
. Disso segue que  em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.