 por thiagoilh » Seg Jan 24, 2011 15:38
por thiagoilh » Seg Jan 24, 2011 15:38
Estou com duvida na resolução de integrais por partes, para esse exemplo:
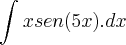
resolvendo só consigo chegar até :
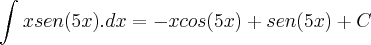
porém o resultado dessa integral é :
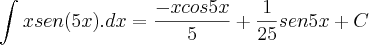
Por favor quem poder me ajudar!!! Como chega nessas frações??? fico grato!!!!
É URGENTE!!
-
thiagoilh
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jan 24, 2011 15:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por helenasilva » Seg Jan 24, 2011 18:47
por helenasilva » Seg Jan 24, 2011 18:47
ola e a minha 1ª vez neste forúm e confesso que tou a gostar imenso..
é o seguinte tenho algumas dúvidas quanto a alguns exercicios que ja os tentei resolver..
h(x)=(x^2-1)/(x^2-9) determina:
seja g(x)=2x+1 determina h e o g(x);
e determina os valores de x para os quais h(x)?0;
no exercico anterior comecei por determinar os zeros mas ainda não sei se é assim que se faz agradecia resposta rapida pois é mesmo urgente.
-
helenasilva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 24, 2011 17:57
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por helenasilva » Seg Jan 24, 2011 18:58
por helenasilva » Seg Jan 24, 2011 18:58
Outra questão é a seguinte:
O que se prentende num exercicio que pede para caracterizar as funções??
aparece : Considera as funções reais de variável f(x)=x^2-1 e g(x)=1/x caracteriza as funções:
a) f+g
b) f x g
c) f/g
Não entendo que se pretende com caracteriza as funções!! Na 1ª chegei ate (f+g)= (x^3-x+1)/x agora não sei como caracterizar las podem me ajudar?? URGENTEMENTE..
-
helenasilva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 24, 2011 17:57
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Seg Jan 24, 2011 22:08
por MarceloFantini » Seg Jan 24, 2011 22:08
Helena, ficamos felizes em saber que você gosta do fórum, mas por favor siga as regras: crie um novo tópico para cada uma das suas dúvidas. Você não respondeu a dúvida do Thiago e ainda por cima colocou outras duas não relacionadas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8866 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2818 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2445 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2534 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2140 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
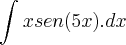
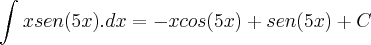
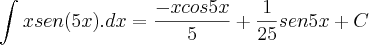

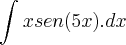
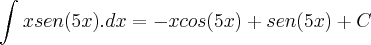
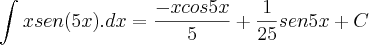







 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.