A)
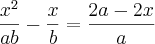
bom , a minha duvida é como encontrar a outra raiz dessa equaçao ,
já q tem tudas possíveis raizes pra esta equação !
eu vou postar como eu encontrei uma .
B)
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
essa eu nem consegui encontrar nenhuma raiz .

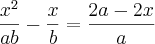
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)

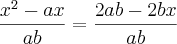
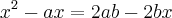

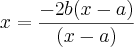

![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
![a=1 ; b= -a\sqrt[]{2x} ; c= -\frac{3}{2}a^2 a=1 ; b= -a\sqrt[]{2x} ; c= -\frac{3}{2}a^2](/latexrender/pictures/d6ca2f3aa91588840034fdc4cc230beb.png)
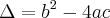
![\Delta=\left(-a\sqrt[]{2x} \right)^2-4.1.\frac{-3}{2}a^2 \Delta=\left(-a\sqrt[]{2x} \right)^2-4.1.\frac{-3}{2}a^2](/latexrender/pictures/c2dee4f5ab81e9da319eb5d6332d2c3a.png)
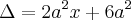
![\Delta=\sqrt[]{2a^2x+6a^2} \Delta=\sqrt[]{2a^2x+6a^2}](/latexrender/pictures/623101573d0d07144c9c1174404c01e7.png)
![\Delta=a^2\sqrt[]{2x+6} \Delta=a^2\sqrt[]{2x+6}](/latexrender/pictures/8303ab806ac0e74f0d65f389656a3881.png)
![\frac{-b+-\sqrt[]{\Delta}}{2a} \frac{-b+-\sqrt[]{\Delta}}{2a}](/latexrender/pictures/615dbc601d72ae78498ba5afd7ae9767.png)
![\rightarrow x^1=\frac{a\sqrt[]{2x}+a^2\sqrt[]{2x+6}}{2} \rightarrow x^1=\frac{a\sqrt[]{2x}+a^2\sqrt[]{2x+6}}{2}](/latexrender/pictures/d3b986dfb2b76180f8f24ba532b17af3.png)
![\rightarrow x^2=\frac{a\sqrt[]{2x}-(a^2\sqrt[]{2x+6})}{2} \rightarrow x^2=\frac{a\sqrt[]{2x}-(a^2\sqrt[]{2x+6})}{2}](/latexrender/pictures/2c80c30402dd4dd4a21c2d4e45a91243.png)

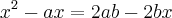


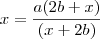




stanley tiago escreveu:entendi obrigado .
e enquanto a alternativa B) , como q fica ?
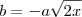 :
:stanley tiago escreveu:
B)
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
![a=1 ; b= -a\sqrt[]{2} ; c= -\frac{3}{2}a^2 a=1 ; b= -a\sqrt[]{2} ; c= -\frac{3}{2}a^2](/latexrender/pictures/31482050f235b6ab4d711f86a6ec38e7.png)




Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)