![\sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png "\sqrt[]{10}")
pertence aos Irracionais?esta coorreto
por Jaison Werner » Qua Jan 19, 2011 09:06
pertence aos Irracionais?
por Renato_RJ » Qua Jan 19, 2011 10:51
por VtinxD » Qua Jan 19, 2011 14:52
![\sqrt[]{10}\in Q](/latexrender/pictures/06686342582ad71fa50a2d77cea79b80.png "\sqrt[]{10}\in Q")
e chega a uma contradição,chegando a conclusão de que ele só pode ser irracional:,então:
e 
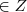e mdc(a;b)=1![\sqrt[]{10}=\frac{a}{b}\Rightarrow {\sqrt[]{10}}^{2}={\frac{a}{b}}^{2}\Rightarrow 10=\frac{{a}^{2}}{{b}^{2}}\Rightarrow](/latexrender/pictures/55356a00c0720f498776303c7898cae3.png "\sqrt[]{10}=\frac{a}{b}\Rightarrow {\sqrt[]{10}}^{2}={\frac{a}{b}}^{2}\Rightarrow 10=\frac{{a}^{2}}{{b}^{2}}\Rightarrow")
.Que implica que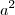 
é par e multiplo de 5, por consequência também é par e multiplo de cinco,visto que e pertencem aos inteiros e diferente de zero.Se é par então pode ser represantado por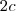 
,logo:
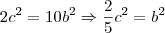.Como é multipo de 5 ,
também é , e como também é inteiro, é par que é um absurdo visto que mdc entre e é igual a 1.
por Debora Bruna » Seg Jan 11, 2016 17:44
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)