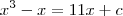por OtavioBonassi » Qua Jan 05, 2011 22:40
por OtavioBonassi » Qua Jan 05, 2011 22:40
"A equação da reta paralela à reta y=11x e tangente ao gráfico de f(x) = x³ - x , num ponto de abscissa negativa , é :"
a) y = 11x + 4
b) y = 11x + 7
c) y = 11x + 10
d) y = 11x + 13
e) y = 11x + 16
Não tenho nem idéia de como chegar em alguma dessas respostas ... Ok , sei o coeficiente angular dessa reta, vai ser 11 , aplico no Mixôxô
( y - yo = m (x - xo) , onde m é o coef. angular) , mas como achar o resto do exercicio nao faço nem idéia ,tentei desenhar os gráficos mas pelo meu desenho tem infinitos pontos aonde a reta pode interceptar f(x).
Obrigado pela ajuda,
Otávio.
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por 0 kelvin » Qui Jan 06, 2011 12:45
por 0 kelvin » Qui Jan 06, 2011 12:45
Mixôxô risos... nunca aprendi essas dicas de memorização da equação da reta, eu sempre me lembro do Pitágoras nessa.
Num ponto de abcissa negativa então esta à esquerda do eixo y. a > 0 então é positivo para a direita da raiz e negativo para a esquerda, função crescente.
A função dada é cúbica e se tem um ponto de tangência então tem um sistema de equações com uma única solução.
Pela definição da função f(x) = y, deve dar então
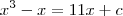
Daí não sei, relações de Girard (soma e multiplicação das raízes)?
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por OtavioBonassi » Qui Jan 06, 2011 20:18
por OtavioBonassi » Qui Jan 06, 2011 20:18
"Num ponto de abcissa negativa então esta à esquerda do eixo y. a > 0 então é positivo para a direita da raiz e negativo para a esquerda, função crescente."
porque ele é necessariamente positiva para a direita da raiz e negativa pra esquerda ? a reta que tangencia um ponto de abscissa negativa pode tanto tangenciar um ponto no 2 quanto no 3° quadrante.
Quando voce "soma" assim (no exemplo 11x + C) voce "eleva" a reta pelo eixo Y ,entao eu preciso descobrir em que ponto ela tangencia, sabendo isso eu posso fazer a eq. da reta ... agora nao sei se as relações de girard ajudariam, até porque nao lembro delas shuahasu se voce pudesse falar como elas são ,per favore hehe ...
Mas não sei se é por ai, eu tava pensando em só achar esse ponto de tangencia mesmo, porque a partir dele posso achar tudo, agora , como achar só esse maldito x em comum ,ai eu já nao sei ...
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por OtavioBonassi » Qui Jan 06, 2011 20:43
por OtavioBonassi » Qui Jan 06, 2011 20:43
Já consegui resolver ,obrigado !
Era só lembrar que o coef. angular do ponto de f(x) tangenciado pela reta era igual a da reta, ou seja , 11.
Foi só igualar a derivada de f(x) a 11 e achar o par ordenado ,e ai então fazer o Mixôxô !
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dedução
por Guilherme Carvalho » Qua Ago 10, 2011 22:40
- 1 Respostas
- 1672 Exibições
- Última mensagem por Molina

Qua Ago 10, 2011 23:49
Trigonometria
-
- Dedução
 por silvanuno11 » Ter Mar 27, 2012 13:26
por silvanuno11 » Ter Mar 27, 2012 13:26
- 0 Respostas
- 1005 Exibições
- Última mensagem por silvanuno11

Ter Mar 27, 2012 13:26
Álgebra Elementar
-
- Dedução de formula
por rodrigosoaresd » Ter Ago 14, 2012 14:30
- 1 Respostas
- 1711 Exibições
- Última mensagem por e8group

Ter Ago 14, 2012 15:34
Geometria Analítica
-
- Dedução da área do círculo.
por Civil UFSCar » Ter Jun 21, 2011 13:24
- 2 Respostas
- 2907 Exibições
- Última mensagem por LuizAquino

Ter Jun 21, 2011 16:08
Cálculo: Limites, Derivadas e Integrais
-
- [Dedução Natural] Exercício
por AlexandreJML » Ter Mar 27, 2012 13:16
- 0 Respostas
- 1577 Exibições
- Última mensagem por AlexandreJML

Ter Mar 27, 2012 13:16
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.